��Ŀ����
����Ŀ����ͼ��ʾ������Ϊ![]() ������ƽ����Ϊ����I��II��III������I��III����ǿ�ų������ǵĴŸ�Ӧǿ�ȴ�С��ȣ�����ֱֽ�����෴������Ϊ
������ƽ����Ϊ����I��II��III������I��III����ǿ�ų������ǵĴŸ�Ӧǿ�ȴ�С��ȣ�����ֱֽ�����෴������Ϊ![]() ����Ϊ
����Ϊ![]() �ľ���abcd���ڴų��·�����ų��߽���룬OΪdc���е㣬PΪdc���д�����һ�㣬OP=3L������������ǿ�糡���糡ǿ�ȴ�СΪE��������aָ��O�������Ϊq������Ϊm���������ƵĴ���������a�㾲ֹ�ͷţ����糡���ٺ����ų����˶��켣�պ�������III���ұ߽����С�
�ľ���abcd���ڴų��·�����ų��߽���룬OΪdc���е㣬PΪdc���д�����һ�㣬OP=3L������������ǿ�糡���糡ǿ�ȴ�СΪE��������aָ��O�������Ϊq������Ϊm���������ƵĴ���������a�㾲ֹ�ͷţ����糡���ٺ����ų����˶��켣�պ�������III���ұ߽����С�
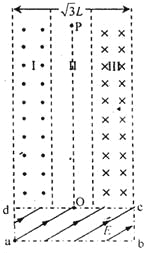
��1��������Ӿ���O��ʱ�ٶȴ�С![]() ��
��
��2������ǿ�ų��ĴŸ�Ӧǿ�ȴ�СB��
��3������aO֮���O��x����ֹ�ͷŸ����ӣ������ڴų������й�ƫתn�ε���P�㣬��x����������Լ�n�Ŀ���ȡֵ��
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]() ������n=2��3��4��5��6��7��8
������n=2��3��4��5��6��7��8
�������������������1���������֪aO=L��������aO���ٹ�����
���ܶ�����![]() �� �����Ӿ���O��ʱ���ٶȴ�С��
�� �����Ӿ���O��ʱ���ٶȴ�С��![]() ��
��
��2�������ڴų�����III�е��˶��켣��ͼ�������ӹ켣�뾶Ϊ![]()


���ݼ��ι�ϵ�ɵ�![]() ��
��
������������ʽ��ţ�ٵڶ����ɿɵ�![]() ���������ڢۢ��ɵ�
���������ڢۢ��ɵ�![]() ��
��
��3���������ڴų���һ������n��ƫת����P�������ӹ켣Բ�뾶ΪR��
���ݼ��ι�ϵ�ɵ�![]() ����������ɵ�
����������ɵ�![]()
�����ۢޢ��ɵ�![]() ����nȡ��������
����nȡ��������
�������ڴų��е��˶�����Ϊv����![]() ��
��
�ڵ糡�еļ��ٹ��̣��ɶ��ܶ�����![]() ��
��
�����ɵ�![]() ������n=2��3��4��5��6��7��8
������n=2��3��4��5��6��7��8

����Ŀ�����õ������͵�ѹ���ⶨһ�ڸɵ�صĵ綯�ƺ��ڵ��衣Ҫ������Сʵ������1��Ӧ��ѡ���ʵ���·��ͼ�е�________��ѡ��������������������


��2�����е�������0��0.6A�������غ͵������ɣ��Լ��������ģ�
A����ѹ����0��15V�� B����ѹ����0��3V��
C��������������0��50���� D��������������0��500����
ʵ���е�ѹ��Ӧѡ��________������������Ӧѡ��__________��ѡ����Ӧ����ǰ����ĸ����
��3��ijͬѧ��¼��6���������±���ʾ������5�����ݵĶ�Ӧ���Ѿ�����ͼ2������ֽ�ϣ���������һ�����ݵĶ�Ӧ�㣬������U-Iͼ�ߡ�
��� | 1 | 2 | 3 | 4 | 5 | 6 |
��ѹU��V�� | 1.45 | 1.40 | 1.30 | 1.25 | 1.20 | 1.10 |
����I��A�� | 0.060 | 0.120 | 0.240 | 0.260 | 0.360 | 0.480 |
��4�����ݣ�3��������ͼ�߿ɵó��ɵ�صĵ綯��E=____V���ڵ���r=_____ ![]()