题目内容
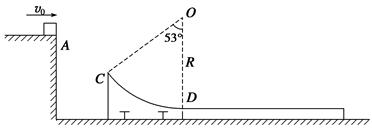
(16分)在竖直平面内固定一轨道ABCO, AB段水平放置,长为4 m,BCO段弯曲且光滑,轨道在O点的曲率半径为1.5 m;一质量为1.0 kg、可视作质点的圆环套在轨道上,圆环与轨道AB段间的动摩擦因数为0.5。建立如图所示的直角坐标系,圆环在沿x轴正方向的恒力F作用下,从A(-7,2)点由静止开始运动,到达原点O时撤去恒力F,水平飞出后经过D(6,3)点。重力加速度g取10m/s2,不计空气阻力。求:
⑴圆环到达O点时对轨道的压力;
⑵恒力F的大小;
⑶圆环在AB段运动的时间。
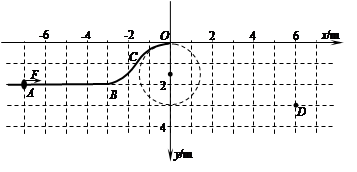
⑴圆环到达O点时对轨道的压力;
⑵恒力F的大小;
⑶圆环在AB段运动的时间。
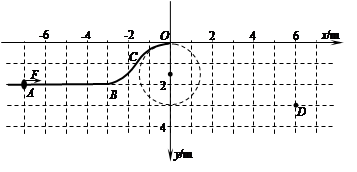
(1)30N,方向竖直向上 (2)F=10N (3)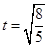
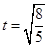
试题分析:(1)圆环从O到D过程中做平抛运动
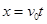 (1分)
(1分) 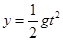 (1分)
(1分) 读图知:x=6m、y=3m, 所以 v0=
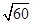 m/s (1分)
m/s (1分) 到达O点时:根据向心力公式
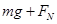 =
=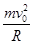 (2分)
(2分) 代入数据,得 FN=30N (1分)
根据牛顿第三定律得,对轨道的压力为30N,方向竖直向上 (1分)
(2)圆环从A到O过程中,根据动能定理 有
 (3分)
(3分)代入数据,得F=10N (1分)
(3)圆环从A到B过程中,根据牛顿第二定律 有
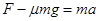 (2分)
(2分)根据运动学公式 有
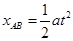 (2分)
(2分)代入数据,得时间
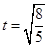 s (1分)
s (1分)
练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
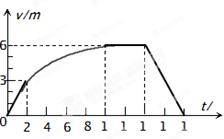


 ,处于磁感应强度为B方向垂直于导轨平面的匀强磁场中.一质量为m、长为L、电阻为R1的导体棒ab放在导轨上,与导轨垂直且接触良好,不计导轨电阻.
,处于磁感应强度为B方向垂直于导轨平面的匀强磁场中.一质量为m、长为L、电阻为R1的导体棒ab放在导轨上,与导轨垂直且接触良好,不计导轨电阻.
 。小球运动到环的最高点时与环恰无作用力,小球从最低点运动到最高点的过程中( )
。小球运动到环的最高点时与环恰无作用力,小球从最低点运动到最高点的过程中( )

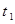 时刻物块才开始运动,(最大静摩擦力与动摩擦力可认为相等),则:( )
时刻物块才开始运动,(最大静摩擦力与动摩擦力可认为相等),则:( )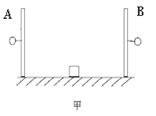
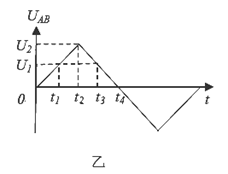
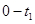 时间内,物块受到逐渐增大的摩擦力,方向水平向右
时间内,物块受到逐渐增大的摩擦力,方向水平向右