题目内容
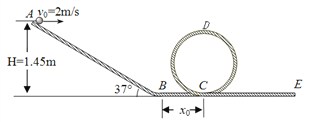
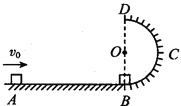
【题目】如图所示，水平地面上相距x=40m的A、B两点，分别放有质量为m1=2kg和m2=1kg的甲、乙两物体（均视为质点），甲与水平地面间的动摩擦因数为
=0.5，BCD是半径为R=0.9m的光滑半圆轨道，O是圆心，DOB在同一竖直线上。甲以v0=25m/s的水平速度从A点向右运动，与静止在B点的乙发生碰撞，碰后粘在一起沿轨道BCD运动，从最高点D飞出，落在水平地面上的P点（图中未画出），取g=10m/s2，求：
（1）甲运动到B点时的速度大小；
（2）甲与乙碰撞过程中系统损失的机械能；
（3）落地点P与B点间的距离。
【答案】（1）15m/s（2）75J（3）4.8m
【解析】
（1）甲从A到B过程由动能定理有：
解得 甲运动到B点时的速度大小
（2）甲和乙碰撞过程中，系统的动量守恒，
则
系统损失的机械能
解得
（3）组合体从B到D过程由动能定理有
组合体从D到P做平抛运动，则
水平方向有：
竖直方向有：
联立解得落地点P与B点间的距离
练习册系列答案
阅读快车系列答案
相关题目
【题目】在“测定匀变速直线运动的加速度”的实验中，打点计时器使用的交流电的频率为50 Hz，记录小车做匀变速运动的纸带如图所示，在纸带上选择0、1、2、3、4、5六个计数点，相邻两计数点之间还有四个点未画出，纸带旁并排放着带有最小分度为毫米的刻度尺，刻度尺的零点跟“0”计数点对齐，由图读出三个计数点1、3、5到0点的距离d1、d2、d3，填入下列表格中．
距离 | d1 | d2 | d3 |
测量值/cm | ___ | ___ | ___ |
计算小车通过计数点“2”的瞬时速度为v2＝___ m/s；小车的加速度是a＝________ m/s2(保留两位有效数字)．
