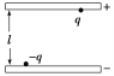
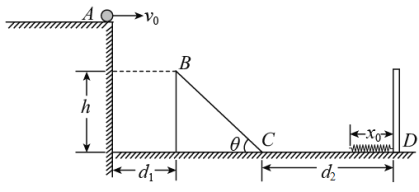
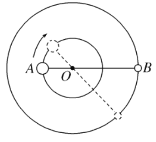
[题目]如图所示.重10N的滑块在倾角为30°的斜面上.从a点由静止开始下滑.到b点开始压缩轻弹簧.到c点时达到最大速度.到d点(图中未画出)开始弹回.返回b点离开弹簧.恰能再回到a点.若bc=0.1m.弹簧弹性势能的最大值为8J.则下列说法正确的是()A.轻弹簧的劲度系数是50N/mB.从d到b滑块克服重力做功8JC.滑块的动能最大值为8JD 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图所示，重10N的滑块在倾角为30°的斜面上，从a点由静止开始下滑，到b点开始压缩轻弹簧，到c点时达到最大速度，到d点(图中未画出)开始弹回，返回b点离开弹簧，恰能再回到a点。若bc=0.1m，弹簧弹性势能的最大值为8J，则下列说法正确的是()

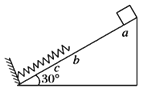
A.轻弹簧的劲度系数是50N/m

B.从d到b滑块克服重力做功8J

C.滑块的动能最大值为8J

D.从d点到b点物体的动能增加量小于弹性势能减少量

【答案】AD

【解析】

滑块先加速运动到b，接触弹簧后是继续加速运动，当滑块的合力为零时，速度最大，再向下做减速运动，速度减到零时，弹簧弹性势能最大.选择适当的过程运用动能定理列式求解弹力做功

A．滑块从b点开始压缩弹簧，到c点达到最大速度，说明在c点合外力为零，由牛顿第二定律可知，故A项正确.

B．从d到a，滑块动能变化为零，弹簧对其做的功全部转化为重力势能，所以从d到a克服重力做功8J ，显然从d到b滑块克服重力做功小于8J，故B项错误.

C．c点滑块速度最大，动能最大，从d点到c点弹簧势能变化量小于从d点到b点弹簧势能变化量，即小于8J，从d点到c点弹簧势能变化量转化为滑块的动能和势能，所以在c点滑块动能小于8J，即滑块最大动能小于8J，故C项错误.

D．从d点到b点，减小的弹性势能转化为滑块的动能和重力势能得增加量，故D项正确.

练习册系列答案

A. φA＞φB B. φA＜φB

C. EA＜EB D. EA与EB无法比较

【题目】如图所示，甲、乙两船在同一条河流中同时开始渡河，M，N分别是甲、乙两船的出发点，两船头与河岸均成α角，甲船船头恰好对准N点的正对岸P点，经过一段时间乙船恰好达到P点，如果划船速度大小相同，且两船相遇，不影响各自的航行，下列判断正确的是()

A.甲船也能到达P点

B.两船渡河时间一定相等

C.两船相遇在NP直线上的某点(不在P点)

D.两船不会在渡河中相遇

【题目】如图所示，P是倾角为30°的光滑固定斜面．劲度系数为k的轻弹簧一端固定在斜面底端的固定挡板C上，另一端与质量为m的物块A相连接.细绳的一端系在物体A上，细绳跨过不计质量和摩擦的定滑轮，另一端有一个不计质量的小挂钩．小挂钩不挂任何物体时，物体A处于静止状态，细绳与斜面平行．在小挂钩上轻轻挂上一个质量也为m的物块B后，物块A沿斜面向上运动．斜面足够长，运动过程中B始终未接触地面．已知重力加速度为g，问：

(1)求物块A刚开始运动时的加速度大小a．

(2)设物块A沿斜面上升通过Q点位置时速度最大，求Q点到出发点的距离x0及最大速度vm．

(3)把物块B的质量变为原来的N倍(N>0.5),小明同学认为，只要N足够大，就可以使物块A沿斜面上滑到Q点时的速度增大到2vm，你认为是否正确？如果正确，请说明理由，如果不正确，请求出A沿斜面上升到Q点位置的速度的范围．

【题目】如图所示，P、Q是固定在竖直平面内的一段内壁光滑弯管的两端，P、Q间的水平距离为d。直径略小于弯管内径的小球以速度从P端水平射入弯管，从Q端射出，在穿过弯管的整个过程中小球与弯管无挤压。若小球从静止开始由P端滑入弯管，经时间t恰好以速度从Q端射出。重力加速度为g，不计空气阻力，那么( )

A.B.C.D.

【题目】如图，一充电后的平行板电容器的两极板相距l，在正极板附近有一质量为M、电荷量为q(q>0)的粒子，在负极板附近有另一质量为m、电荷量为－q的粒子，在电场力的作用下，两粒子同时从静止开始运动．已知两粒子同时经过一平行于正极板且与其相距l的平面．若两粒子间相互作用力可忽略，不计重力，则M∶m为( )