��Ŀ����
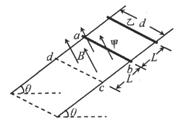
��2012��4���Ĵ�������ģ����ͼ��ʾ�������㹻�������費�ơ����Ϊd�Ĺ⻬ƽ�н������죬������ƽ����ˮƽ��н�Ϊ�ȣ�����ƽ���ڵľ�������abcd�ڴ����н���ǿ�ų����Ÿ�Ӧǿ�ȴ�Сb����ֱ��б�����ϣ�ab��cd֮�����ΪL0�����˼ס��ҵ���ֵ��ͬ��������Ϊm,���ڴų�������ϱ߽�ab�����Ҹ��ڼ��Ϸ�������L�����ס������˶��뵼�촹ֱ����ֹ�ͷ����˵�ͬʱ���ڼ���ʩ��һ����ֱ�ڸ�ƽ���ڵ��������F��ʹ�����дų��ľ����������������ȼ���ֱ���˶������ٶȴ�С![]() ���뿪�ų�ʱ��ȥF���Ҹ˽���ų���ǡ���������˶���Ȼ���뿪�ų���
���뿪�ų�ʱ��ȥF���Ҹ˽���ų���ǡ���������˶���Ȼ���뿪�ų���
(1 )��ÿ�������˵ĵ���R�Ƕ��
(2 )���ͷŽ����˿�ʼ��ʱ��������F��ʱ��t�ı仯��ϵʽ����˵��F�ķ���
(3 )�����������У��ҽ����˹���������Q��������F�Լ��������Ĺ�W�Ƕ���?
�⣺
(1) ����ڴų�����abcd���˶�ʱ��Ϊt1���Ҵӿ�ʼ�˶���abλ�õ�ʱ��Ϊt2����
![]() ��
��![]()
![]() ��
��![]() 1��
1��
t1��t2�������뿪�ų�ʱ���һ�û�н���ų��� 1��
���ҽ���ų�ʱ���ٶ�Ϊv1�����еĸ�Ӧ�綯��ΪE1����·�еĵ���ΪI1����
![]() 1��
1��
E1= Bdv1 1��
I1=E1/2R 1��
mgsin�� = BI1d 1��
���![]() 1��
1��
(2) ���ͷŽ����˿�ʼ��ʱ���辭��ʱ��t�����ٶ�Ϊv�����еĸ�Ӧ�綯��ΪE����·�еĵ���ΪI������ΪF����
v= at 1��
E= Bdv 1��
I=E/2R 1��
F +mgsin�ȣ�BId = ma 1��
a = 2gsin��
���![]() ��0��t��
��0��t��![]() �� 1��
�� 1��
����ֱ�ڸ�ƽ���ڵ������¡� 1��
(3) ���ڴų����˶������У���û�н���ų�������뿪�ų�ʱ�ٶ�Ϊv0�����ص����˶��ľ�����x���ס��Ҳ�����������ͬ����ֱ�ΪQ1����
![]() 1��
1��
![]() 2��
2��
���![]()
���ڴų����˶������У����Ҳ�����ͬ����������ֱ�ΪQ 2����
2Q2 = mgLsin�� 2��
����������Q = Q1 + Q2 1��
��� W = 2Q 1��