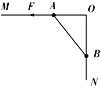
题目内容
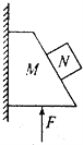
【题目】如图所示,两光滑直杆成直角竖直固定,OM水平,ON竖直,两个质量相同的有孔小球A、B(可视为质点)串在杆上通过长为L的非弹性轻绳相连,开始时小球A在水平向左的外力作用下处于静止状态,此时OB=![]() ,重力加速度为g,现将外力增大到原来的4倍(方向不变),则小球B运动到与O点的距离为
,重力加速度为g,现将外力增大到原来的4倍(方向不变),则小球B运动到与O点的距离为![]() 时的速度大小为
时的速度大小为
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】C
【解析】开始时A到O的距离:![]()
以B为研究对象,开始时B受到重力、杆的支持力N和绳子的拉力T,如图,则: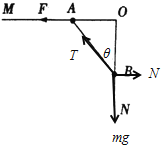
tanθ=![]() ;由几何关系:tanθ=
;由几何关系:tanθ=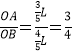 ;联立得:N=
;联立得:N=![]() mg
mg
以AB组成的整体为研究对象,在水平方向二者受到拉力F和杆对B的支持力N,由于水平方向受力平衡,所以F=N=![]() mg
mg
现将外力增大到原来的4倍(方向不变),则:F′=4F=3mg
B球向上运动时,小球B运动到O点的距离![]() L时,由几何关系得,A到O点的距离:
L时,由几何关系得,A到O点的距离:
OA′=![]()
A向右的距离:![]()
B上升的距离: ![]()
此时细绳与竖直方向之间夹角的正切值:tanθ′=![]() ,则得 cosθ′=0.6,sinθ′=0.8
,则得 cosθ′=0.6,sinθ′=0.8
由运动的合成与分解知识可知:A球的受到与B球的速度之间的关系为为:vBcosθ′=vAsinθ′
可得 vB=![]() vA
vA
以AB球组成的整体为研究对象,拉力和重力对系统做功,由动能定理得:
F′△Smg△h=![]()
联立以上方程解得:vB=![]()
选项C正确。故选C.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目