题目内容
13. 如图所示,直角坐标系xoy位于竖直平面内,在?$\sqrt{3}$m≤x≤0的区域内有磁感应强度大小B=4.0×10-4T、方向垂直于纸面向里的条形匀强磁场,其左边界与x轴交于P点;在x>0的区域内有电场强度大小E=4N/C、方向沿y轴正方向的条形匀强电场,其宽度d=2m.一质量m=6.4×10-27kg、电荷量q=-3.2×10?19C的带电粒子从P点以速度v=4×104m/s,沿与x轴正方向成α=60°角射入磁场,经电场偏转最终通过x轴上的Q点(图中未标出),不计粒子重力.求:
如图所示,直角坐标系xoy位于竖直平面内,在?$\sqrt{3}$m≤x≤0的区域内有磁感应强度大小B=4.0×10-4T、方向垂直于纸面向里的条形匀强磁场,其左边界与x轴交于P点;在x>0的区域内有电场强度大小E=4N/C、方向沿y轴正方向的条形匀强电场,其宽度d=2m.一质量m=6.4×10-27kg、电荷量q=-3.2×10?19C的带电粒子从P点以速度v=4×104m/s,沿与x轴正方向成α=60°角射入磁场,经电场偏转最终通过x轴上的Q点(图中未标出),不计粒子重力.求:(1)带电粒子在磁场中运动时间;
(2)当电场左边界与y轴重合时Q点的横坐标;
(3)若只改变上述电场强度的大小,要求带电粒子仍能通过Q点,讨论此电场左边界的横坐标x′与电场强度的大小E′的函数关系.
分析 (1)粒子在匀强磁场中由洛伦兹力提供向心力,做匀速圆周运动,由牛顿第二定律求出半径,作出轨迹,由几何知识找出圆心角,求出运动时间.
(2)粒子进入匀强电场,只受电场力,做类平抛运动,根据运动的分解,求出粒子离开电场时的速度偏向角为θ,由数学知识求出Q点的横坐标.
(3)讨论当0<x′<3m时,Q点在电场外面右侧,画出轨迹,研究速度偏向角,求出横坐标x′与电场强度的大小E′的函数关系.
当3m≤x'≤5m时,Q点在电场里,画出轨迹,研究偏转距离y,求出横坐标x′与电场强度的大小E′的函数关系.
解答 解:(1)带电粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:$qvB=\frac{{m{v^2}}}{r}$,代入数据得:r=2m,
轨迹如图1交y轴于C点,过P点作v的垂线交y轴于O1点,
由几何关系得O1为粒子运动轨迹的圆心,且圆心角为60°.
在磁场中运动时间:$t=\frac{T}{6}=\frac{1}{6}×\frac{2πm}{qB}$,代入数据得:t=5.23×10-5s;
(2)带电粒子离开磁场垂直进入电场后做类平抛运动,
设带电粒子离开电场时的速度偏向角为θ,如图1,
则:$tanθ=\frac{v_y}{v}=\frac{Eqd}{{m{v^2}}}=\frac{{4×3.2×{{10}^{-19}}×2}}{{6.4×{{10}^{-27}}×16×{{10}^8}}}=\frac{1}{4}$,
设Q点的横坐标为x,则:$tanθ=\frac{1}{x-1}=\frac{1}{4}$,解得:x=5m.
(3)电场左边界的横坐标为x′.
当0<x′<3m时,如图2,设粒子离开电场
时的速度偏向角为θ′,
则:$tanθ'=\frac{E'qd}{{m{v^2}}}$,
又:$tanθ'=\frac{1}{4-x'}$,
由上两式得:$E'=\frac{16}{4-x'}$,
当3m≤x'≤5m时,如图3,有:
$y=\frac{1}{2}a{t^2}=\frac{{E'q{{(5-x')}^2}}}{{2m{v^2}}}$,
将y=1m及各数据代入上式得:$E'=\frac{64}{{{{(5-x')}^2}}}$;
答:(1)带电粒子在磁场中运动时间为t=5.23×10-5s.
(2)当电场左边界与y轴重合时Q点的横坐标x=5m.
(3)电场左边界的横坐标x′与电场强度的大小E′的函数关系为:当0<x′<3m时,E′=$\frac{16}{4-x′}$,
当3m≤x'<5m时,E′=$\frac{64}{(5-x′)^{2}}$;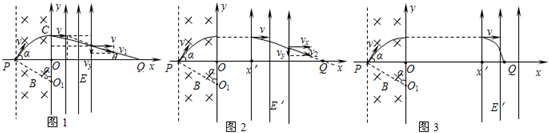
点评 本题是磁场和电场组合场问题,考查分析和解决综合题的能力,关键是运用几何知识画出粒子的运动轨迹.

 阅读快车系列答案
阅读快车系列答案| A. | 甲、乙两球距离越来越大,但甲、乙两球速度之差保持不变 | |
| B. | 甲、乙两球距离越来越大,且甲、乙两球速度之差越来越大 | |
| C. | 甲、乙两球距离始终保持不变,且甲、乙两球速度之差保持不变 | |
| D. | 甲、乙两球距离越来越小,且甲、乙两球速度之差越来越小 |
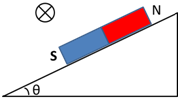 如图所示,条形磁铁放在倾斜桌面上,在其上方固定一根长直导线,导线与磁铁垂直,给导线通以垂直纸面向内的电流,则( )
如图所示,条形磁铁放在倾斜桌面上,在其上方固定一根长直导线,导线与磁铁垂直,给导线通以垂直纸面向内的电流,则( )| A. | 磁铁对桌面压力减小,可能受到桌面的摩擦力作用 | |
| B. | 磁铁对桌面压力减小,一定受到桌面的摩擦力作用 | |
| C. | 磁铁对桌面压力增大,可能受到桌面的摩擦力作用 | |
| D. | 磁铁对桌面压力增大,一定受到桌面的摩擦力作用 |
| A. | 光敏电阻 | B. | 压敏电阻 | C. | 热敏电阻 | D. | 力敏电阻 |
| A. | 在三峡高中16届田径运动会中,运动员跑完200m位移的大小和路程不相等 | |
| B. | 三峡高中12:50学生开始午休,其中“12:50”指的是时间 | |
| C. | 平均速率等于平均速度的大小 | |
| D. | 速率为瞬时速度的大小,速度是标量 |
| A. | 它的发射速度不可能小于7.9km/s | |
| B. | 已知它的质量是1.42T,若将它的质量增为2.84T,其同步轨道的半径变为原来的2倍 | |
| C. | 它可以绕过成都的正上方,所以可以利用它转播四川电视台的节目 | |
| D. | 它距地面的高度约是地球半径的5倍,所以它的向心加速度约是地面处的重力加速度的$\frac{1}{25}$ |
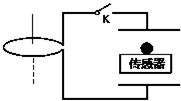 如图所示,两块金属板水平放置,与左侧水平放置的线圈通过开关K用导线连接.压力传感器上表面绝缘,位于两金属板间,带正电的小球静置于压力传感器上,变化的磁场沿线圈的轴向穿过线圈.K未接通时传感器的示数为1N,K闭合后传感器的示数稳定为2N.则磁场的变化情况可能是(设磁场向上为正方向)( )
如图所示,两块金属板水平放置,与左侧水平放置的线圈通过开关K用导线连接.压力传感器上表面绝缘,位于两金属板间,带正电的小球静置于压力传感器上,变化的磁场沿线圈的轴向穿过线圈.K未接通时传感器的示数为1N,K闭合后传感器的示数稳定为2N.则磁场的变化情况可能是(设磁场向上为正方向)( )