题目内容
8. 如图所示,在xOy平面的第一象限有一匀强电场,电场的方向平行于y轴向下,电场的大小为E(未知).在x轴和第四象限的射线OC之间有一匀强磁场,磁感应强度的大小为B(未知),方向垂直于纸面向外.有一质量为m,带有电荷量+q的质点以速率v0由y轴上P点平行于x轴射入电场,质点到达x轴上A点时速率为2v0,速度方向与x轴的夹角为φ(未知),A点与原点O的距离为d,接着质点进入磁场,并垂直于OC飞离磁场,不计重力影响,若OC与x轴的夹角也为φ,求
如图所示,在xOy平面的第一象限有一匀强电场,电场的方向平行于y轴向下,电场的大小为E(未知).在x轴和第四象限的射线OC之间有一匀强磁场,磁感应强度的大小为B(未知),方向垂直于纸面向外.有一质量为m,带有电荷量+q的质点以速率v0由y轴上P点平行于x轴射入电场,质点到达x轴上A点时速率为2v0,速度方向与x轴的夹角为φ(未知),A点与原点O的距离为d,接着质点进入磁场,并垂直于OC飞离磁场,不计重力影响,若OC与x轴的夹角也为φ,求(1)φ=60°;
(2)匀强电场的场强大小E=$\frac{\sqrt{3}m{v}_{0}^{2}}{qd}$;
(3)磁感应强度的大小B=$\frac{4\sqrt{3}m{v}_{0}}{3qd}$.
分析 (1)带电粒子在电场中做类平抛运动,根据类平抛运动规律由速度的合成与分解求得夹角的大小;
(2)由平抛运动规律粒子在电场中的加速度,再根据牛顿第二定律求得电场强度的大小;
(3)作出粒子在磁场中的运动轨迹,再根据几何关系求得粒子在磁场中圆周运动的半径根据洛伦兹力提供圆周运动向心力求得磁感应强度的大小.
解答 解:(1)质点在电场中在电场力作用下做类平抛运动,质点在P点的速率为v0,方向平行于x轴射入电场,在A点时的速率为2v0,则有:
$\frac{{v}_{P}}{{v}_{A}}=\frac{{v}_{0}}{2{v}_{0}}=cosφ$
所以可得φ=60°
(2)设从P点到A点类平抛运动的时间为t,
则有${v}_{A}=\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$
可得质点离开电场时${v}_{y}=\sqrt{3}{v}_{0}$
水平方向有:d=v0t
可得粒子运动时间:t=$\frac{d}{{v}_{0}}$
竖直方向有:$y=\frac{\sqrt{3}}{2}{v}_{0}t=\frac{\sqrt{3}}{2}d$
又在竖直方向:$y=\frac{1}{2}a{t}^{2}=\frac{1}{2}•\frac{qE}{m}{t}^{2}$
联立解得:E=$\frac{\sqrt{3}m{v}_{0}^{2}}{qd}$
(3)质点在磁场中运动的轨迹如右图所示
质点运动轨迹为一圆弧,质点飞离磁场时,速度垂直于OC,故圆弧的圆心在OC上,依题意,质点轨迹与x轴的交点为A,过A点作与A点速度方向垂直的直线与OC交于O',由几何关系知,AO'垂直于OC,O'是圆弧的圆心,设圆弧的半径为R则有:
R=dsinφ=$\frac{\sqrt{3}}{2}d$
由洛伦兹力提供圆周运动向心力有:
$qvB=m\frac{{v}^{2}}{R}$
可得B=$\frac{mv}{qR}$=$\frac{4\sqrt{3}m{v}_{0}}{3qd}$
故答案为:60°;$\frac{\sqrt{3}m{v}_{0}^{2}}{qd}$;$\frac{4\sqrt{3}m{v}_{0}}{3qd}$.
点评 本题为电荷在电场和磁场中运动的题目,在电场中的运动一般以平抛为主,而在圆周运动中主要考查匀速圆周运动,应注意找出圆心和半径;同时要注意题目中哪些为已知量哪些为未知量.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 如图所示,水平放置的传送带足够长,它以恒定速率v逆时针运行,一小物体以水平向右的初速度v0滑上A端,物体与传送带间的动摩擦因数为μ.物体离开传送带前,以下说法正确的是( )
如图所示,水平放置的传送带足够长,它以恒定速率v逆时针运行,一小物体以水平向右的初速度v0滑上A端,物体与传送带间的动摩擦因数为μ.物体离开传送带前,以下说法正确的是( )| A. | 如果v0=v,物体一定受到摩擦力的作用 | |
| B. | 如果v0>v,物体将先减速运动再匀速运动 | |
| C. | 如果v0<v,物体将先向右做减速运动再向左做加速运动 | |
| D. | 如果v0<v,物体将先加速运动再匀速运动 |
| A. | 沿斜面减速下滑的物体 | B. | 沿光滑斜面自由下滑的物体 | ||
| C. | 从树上落下的树叶 | D. | 匀速下落的降落伞 |
| A. | sA=sB | B. | sA>sB | C. | sA<sB | D. | 不能确定 |
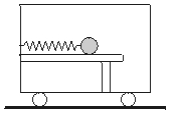 沿平直轨道运动的火车车厢中的光滑水平桌面上用弹簧拴着一个小球,弹簧处于自然长度,如图所示,当旅客看到弹簧的长度变长时,对火车运动状态的判断可能正确的是( )
沿平直轨道运动的火车车厢中的光滑水平桌面上用弹簧拴着一个小球,弹簧处于自然长度,如图所示,当旅客看到弹簧的长度变长时,对火车运动状态的判断可能正确的是( )| A. | 向右运动,速度在增大 | B. | 向右运动,速度在减小 | ||
| C. | 向左运动,速度在增大 | D. | 向左运动,速度在减小 |
 如图所示,固定在竖直平面内的光滑细杆MN,是按照以初速度v0平抛的运动轨迹制成,M端为抛出点,MN间竖直方向高度差为h.现将一小球套于其上,由静止开始从M端沿杆滑下,已知重力加速度为g,则有( )
如图所示,固定在竖直平面内的光滑细杆MN,是按照以初速度v0平抛的运动轨迹制成,M端为抛出点,MN间竖直方向高度差为h.现将一小球套于其上,由静止开始从M端沿杆滑下,已知重力加速度为g,则有( )| A. | 小球做匀变速曲线运动 | |
| B. | 小球从M端运动到N端所需时间等于$\sqrt{\frac{2h}{g}}$ | |
| C. | 运动到N端时,小球速度的水平分量等于$\frac{{v}_{0}\sqrt{2gh}}{\sqrt{2gh+{{v}_{0}}^{2}}}$ | |
| D. | 运动到N端时,小球速度的竖直分量等于$\sqrt{2gh}$ |
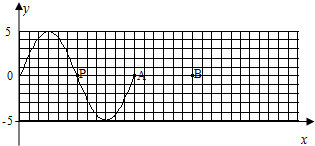 在某介质中形成一列简谐横波,在t=0时刻的波形如图所示,图上每一小格长度为1cm.若波向右传播,t=0时刻刚好传到A点,已知开始计时后,质点P在t1=1.5s时刻第一次到达波谷位置.试求:
在某介质中形成一列简谐横波,在t=0时刻的波形如图所示,图上每一小格长度为1cm.若波向右传播,t=0时刻刚好传到A点,已知开始计时后,质点P在t1=1.5s时刻第一次到达波谷位置.试求: