Question

【题目】如图所示，荧光屏MN与x轴垂直放置，荧光屏所在位置的横坐标x0=60cm，在第一象限y轴和MN之间存在沿y轴负方向的匀强电场，电场强度E=1.6×103N/C，在第二象限有半径R=5cm的圆形磁场，磁感应强度B=0.8T，方向垂直xOy平面向外。磁场的边界和x轴相切于P点。在P点有一个粒子源，可以向x轴上方180°范围内的各个方向发射比荷为=1.0×108C/kg的带正电的粒子，已知粒子的发射速率v0=4.0×106m/s。不考虑粒子的重力、粒子间的相互作用。求：

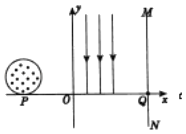
（1）带电粒子在磁场中运动的轨迹半径；

（2）粒子从y轴正半轴上射入电场的纵坐标范围；

（3）带电粒子打到荧光屏上的位置与Q点的最远距离。

Answer 1

【答案】（1）5cm；（2）0≤y≤10cm；（3）9cm。

【解析】

（1）带电粒子进入磁场受到洛伦兹力的作用做圆周运动，由洛伦兹力提供向心力得：

qvB=m

解得：r==5×10﹣2m=5cm

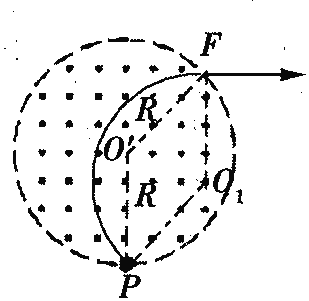
（2）由（1）问可知r=R，取任意方向进入磁场的粒子，画出粒子的运动轨迹如图所示，

由几何关系可知四边形PO′FO1为菱形，所以FO1∥O′P，

又O′P垂直于x轴，粒子出射的速度方向与轨迹半径FO1垂直，则所有粒子离开磁场时的方

向均与x轴平行，所以粒子从y轴正半轴上射入电场的纵坐标范围为0≤y≤10cm

（3）假设粒子没有射出电场就打到荧光屏上，有x0=v0t0，h=，a=

解得：h=18cm＞2R=10cm

说明粒子离开电场后才打在荧光屏上。设从纵坐标为y的点进入电场的粒子在电场中沿x轴方向的位移为x，则x=v0t，y=，代入数据解得：x=

设粒子最终到达荧光屏的位置与Q点的最远距离为H，粒子射出电场时速度方向与x轴正方向间的夹角为θ，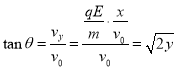

所以H=（x0﹣x）tanθ=（x0﹣）

由数学知识可知，当（x0﹣）=时，即y=4.5cm时H有最大值

所以Hmax=9cm