题目内容
2.在真空中有一个质量为m,带电量为e的电子,以一定速度射入磁感应强度为B的匀强磁场中,当电子以半径R作匀速圆周运动时,突然取消磁场,要使电子继续沿着原轨道以原速率运行,需在圆心处放一个电性为正的电荷Q,其电量为$\frac{e{B}^{2}{R}^{3}}{km}$.分析 电子在磁场中做圆周运动洛伦兹力提供向心力,在点电荷的电场中做圆周运动,库仑力提供向心力,应用牛顿第二定律分析答题.
解答 解:电子绕圆心处的电荷做圆周运动,电荷对电子产生引力作用,则电荷带正电;
电子在磁场中做圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:evB=m$\frac{{v}^{2}}{R}$,
电子在电场中做圆周运动,库仑力提供向心力,由牛顿第二定律得:k$\frac{eQ}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$,
解得:Q=$\frac{e{B}^{2}{R}^{3}}{km}$;
故答案为:正;$\frac{e{B}^{2}{R}^{3}}{km}$.
点评 本题考查了电子做圆周运动问题,知道什么力提供向心力是解题的关键,应用牛顿第二定律、库伦定律可以解题.

练习册系列答案
相关题目
13.下列说法中正确的是( )
| A. | 研究物体的运动时,选不选参考系都可以 | |
| B. | 参考系可以是变速运动的物体 | |
| C. | 研究一列火车通过一座桥梁的时间时,可以把火车看做质点 | |
| D. | 研究跳水运动员的转体动作时,运动员可以视作质点 |
7. 如图所示,OM和ON都在纸面内,且相互垂直,只在MON区域内有垂直于纸面向外的匀强磁场,磁场的磁感应强度大小为B.在OM上的P点有一质量为m、电荷量为-q的带电粒子以一速度沿与OM成θ=45°角方向射入磁场,O、P间距离为L,粒子所受重力不计,则( )
如图所示,OM和ON都在纸面内,且相互垂直,只在MON区域内有垂直于纸面向外的匀强磁场,磁场的磁感应强度大小为B.在OM上的P点有一质量为m、电荷量为-q的带电粒子以一速度沿与OM成θ=45°角方向射入磁场,O、P间距离为L,粒子所受重力不计,则( )
 如图所示,OM和ON都在纸面内,且相互垂直,只在MON区域内有垂直于纸面向外的匀强磁场,磁场的磁感应强度大小为B.在OM上的P点有一质量为m、电荷量为-q的带电粒子以一速度沿与OM成θ=45°角方向射入磁场,O、P间距离为L,粒子所受重力不计,则( )
如图所示,OM和ON都在纸面内,且相互垂直,只在MON区域内有垂直于纸面向外的匀强磁场,磁场的磁感应强度大小为B.在OM上的P点有一质量为m、电荷量为-q的带电粒子以一速度沿与OM成θ=45°角方向射入磁场,O、P间距离为L,粒子所受重力不计,则( )| A. | 带电粒子在磁场中的运动时间可能为$\frac{5πm}{3qB}$ | |
| B. | 带电粒子在磁场中的运动时间可能为$\frac{3πm}{5qB}$ | |
| C. | 带电粒子经过ON的位置到O的距离可能为(3-$\sqrt{2}$)L | |
| D. | 带电粒子经过ON的位置到O的距离可能为(2-$\sqrt{3}$)L |
12.一物体运动的位移与时间关系x=24t-3t2(m)(t以s为单位)则( )
| A. | 这个物体做匀变速运动 | B. | 这个物体的初速度为24m/s | ||
| C. | 这个物体加速度为6m/s2 | D. | 4s末物体离出发点距离为48m |
 如图所示,圆形区域内分布着垂直纸面的匀强磁场,位于磁场边界上P点的粒子源在纸面内沿各个方向以相同的速率向磁场发射同种带电粒子(粒子只受磁场力作用),这些粒子射出边界的位置均分布在边界的某一段弧上,且这段圆弧的弧长是圆周长的$\frac{1}{3}$;若将磁感应强度的大小从B1变为B2,相应的弧长变为圆周长的$\frac{1}{6}$,则$\frac{{B}_{2}}{{B}_{1}}$等于多少?
如图所示,圆形区域内分布着垂直纸面的匀强磁场,位于磁场边界上P点的粒子源在纸面内沿各个方向以相同的速率向磁场发射同种带电粒子(粒子只受磁场力作用),这些粒子射出边界的位置均分布在边界的某一段弧上,且这段圆弧的弧长是圆周长的$\frac{1}{3}$;若将磁感应强度的大小从B1变为B2,相应的弧长变为圆周长的$\frac{1}{6}$,则$\frac{{B}_{2}}{{B}_{1}}$等于多少?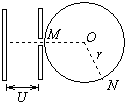 如图所示,离子源从小孔发射出带电量为e的正离子(初速度可忽略),在加速电压U的作用下,沿MO方向进入匀强磁场中,磁场限制在以O点为圆心,半径为r的区域内,磁感应强度为B,方向垂直纸面向外,离子从N点射出,已知∠MON=120°,则正离子质量为$\frac{3e{B}^{2}{r}^{2}}{2U}$,正离子通过磁场所需时间为$\frac{\sqrt{3}πr}{3v}$.
如图所示,离子源从小孔发射出带电量为e的正离子(初速度可忽略),在加速电压U的作用下,沿MO方向进入匀强磁场中,磁场限制在以O点为圆心,半径为r的区域内,磁感应强度为B,方向垂直纸面向外,离子从N点射出,已知∠MON=120°,则正离子质量为$\frac{3e{B}^{2}{r}^{2}}{2U}$,正离子通过磁场所需时间为$\frac{\sqrt{3}πr}{3v}$.