题目内容
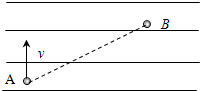 如图所示,质量为m带电量为-q 的微粒(重力不计),在匀强电场中的A点时速度为v,方向与电场线垂直,在B点时速度大小为2v,已知A、B两点间距离为d,求:
如图所示,质量为m带电量为-q 的微粒(重力不计),在匀强电场中的A点时速度为v,方向与电场线垂直,在B点时速度大小为2v,已知A、B两点间距离为d,求:①A、B两点间电压?
②电场强度大小和方向?
分析:(1)微粒重力不计,只受电场力作用,根据动能定理求解A、B两点间电压.
(2)将微粒的运动分解为水平方向和竖直方向,竖直方向做匀速直线运动,水平方向做匀加速直线运动,分别列出两个方向的分位移,求出运动时间,再AB两点沿电场方向的距离,求解电场强度的大小和方向.
(2)将微粒的运动分解为水平方向和竖直方向,竖直方向做匀速直线运动,水平方向做匀加速直线运动,分别列出两个方向的分位移,求出运动时间,再AB两点沿电场方向的距离,求解电场强度的大小和方向.
解答:解:(1)根据动能定理得
-qUAB=
m(2v)2-
mv2
得,UAB=-
(2)微粒在B水平方向的分速度大小为vx=
=
设A、B间水平距离为x,竖直距离为y.
水平方向微粒做匀加速直线运动,则有:
x=
=
竖直方向微粒做匀速直线运动,则有
y=vt
又d2=x2+y2
联立上述三式得,t=
?
x=
=
=
d
则电场强度E=
=
,方向水平向左.
答:
①A、B两点间电压是-
.
②电场强度大小是
,方向水平向左.
-qUAB=
| 1 |
| 2 |
| 1 |
| 2 |
得,UAB=-
| 3mv2 |
| 2q |
(2)微粒在B水平方向的分速度大小为vx=
| (2v)2-v2 |
| 3v |
设A、B间水平距离为x,竖直距离为y.
水平方向微粒做匀加速直线运动,则有:
x=
| vxt |
| 2 |
| ||
| 2 |
竖直方向微粒做匀速直线运动,则有
y=vt
又d2=x2+y2
联立上述三式得,t=
2
| ||
| 7 |
| d |
| v |
x=
| vxt |
| 2 |
| ||
| 2 |
| ||
| 7 |
则电场强度E=
| UAB |
| x |
| ||
| 2qd |
答:
①A、B两点间电压是-
| 3mv2 |
| 2q |
②电场强度大小是
| ||
| 2qd |
点评:本题是类平抛运动,采用运动的合成与分解法,要抓住两个分运动的等时性.中等难度.

练习册系列答案
相关题目
 如图所示一质量为m带电量为+q的带电液滴从水平放置的平行金属板上方H高度处自由落下,从上板的缺口进入两板间电场,电场强度为E,方向竖直向上.若Eq>mg,试求液滴落入电场中所能达到的最大位移h?
如图所示一质量为m带电量为+q的带电液滴从水平放置的平行金属板上方H高度处自由落下,从上板的缺口进入两板间电场,电场强度为E,方向竖直向上.若Eq>mg,试求液滴落入电场中所能达到的最大位移h?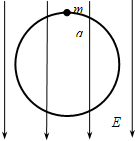 (2009?德阳模拟)如图所示,质量为m带电量为-q的小球穿在半径为R的光滑圆环上,整个装置处在竖直向下的场强为E的匀强电场中时,小球在竖直面内作匀速圆周运动,在最高点小球对环的作用力大小为mg/2.
(2009?德阳模拟)如图所示,质量为m带电量为-q的小球穿在半径为R的光滑圆环上,整个装置处在竖直向下的场强为E的匀强电场中时,小球在竖直面内作匀速圆周运动,在最高点小球对环的作用力大小为mg/2.
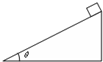 如图所示,质量为m带电荷+q的滑块恰能从倾角为θ的绝缘斜面上匀速下滑.现在斜面所在平面内加一匀强电场使滑块恰能沿斜面匀速上滑,关于所加电场的说法正确的是( )
如图所示,质量为m带电荷+q的滑块恰能从倾角为θ的绝缘斜面上匀速下滑.现在斜面所在平面内加一匀强电场使滑块恰能沿斜面匀速上滑,关于所加电场的说法正确的是( )