题目内容
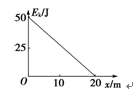
(15分)如图15所示，在水平方向的匀强电场中有一表面光滑、与水平面成45°角的绝缘直杆AC，其下端(C端)距地面高度h＝0.8 m．有一质量为500 g的带电小环套在直杆上，正以某一速度沿杆匀速下滑，小环离开杆后正好通过C端的正下方P点．(g取10 m/s2)求：
(1)小环离开直杆后运动的加速度大小和方向；
(2)小环在直杆上匀速运动时速度的大小；
(3)小环运动到P点的动能．
(1)小环离开直杆后运动的加速度大小和方向；
(2)小环在直杆上匀速运动时速度的大小；
(3)小环运动到P点的动能．
(1)14.1 m/s2，垂直于杆斜向右下方
(2)2 m/s (3)5 J
(2)2 m/s (3)5 J
(1)小环在直杆上的受力情况如图所示．
由平衡条件得：mgsin45°＝Eqcos45°，
得mg＝Eq，
离开直杆后，只受mg、Eq作用，则
F合＝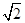
mg＝ma，
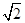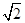a＝g＝10 m/s2≈14.1 m/s2
方向与杆垂直斜向右下方．
(2)设小环在直杆上运动的速度为v0，离杆后经t秒到达P点，则竖直方向：h＝v0sin45°·t＋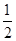
gt2，
水平方向：v0cos45°·t－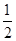
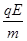t2＝0
解得：v0＝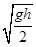
＝2 m/s
(3)由动能定理得：EkP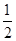－mv02＝mgh
可得：EkP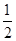＝mv02＋mgh＝5 J.
由平衡条件得：mgsin45°＝Eqcos45°，
得mg＝Eq，
离开直杆后，只受mg、Eq作用，则
F合＝
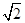mg＝ma，a＝
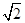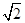g＝10 m/s2≈14.1 m/s2方向与杆垂直斜向右下方．
(2)设小环在直杆上运动的速度为v0，离杆后经t秒到达P点，则竖直方向：h＝v0sin45°·t＋
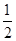gt2，水平方向：v0cos45°·t－
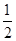
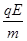t2＝0解得：v0＝
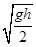＝2 m/s(3)由动能定理得：EkP－
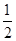mv02＝mgh可得：EkP＝
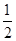mv02＋mgh＝5 J.
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
，则经过t时间，合力的功和最大功率的大小是( )
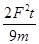
，则电场强度E多大？
