题目内容
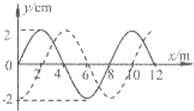 一列沿x轴方向传播的简谐横波,某时刻的波形如图中的实线所示,经过2s后波形如图中虚线所示.求这列波的波速.
一列沿x轴方向传播的简谐横波,某时刻的波形如图中的实线所示,经过2s后波形如图中虚线所示.求这列波的波速.分析:由图读出波长.波向右传播的最短距离为1m,向左传播的最短距离为3m.考虑波的双向性和周期性,分别写出向左传播或向右传播的速度的通项.
解答:解:由图可知:波长λ=8m,若波沿x轴正方向传播:△t=(n+
)T,得 T=
v=
=
=
(4n+1 )=
×(4n+1)m/s=(4n+1)m/s,(n=0,1,2,3…)
同理,若波沿x轴负方向传播:△t=(n+
)T,v=
解得:v=(4n+3)m/s,(n=0,1,2,3…)
答:若波沿x轴正方向传播这列波的波速为(4n+1)m/s,(n=0,1,2,3…),若波沿x轴负方向传播这列波的波速为(4n+3)m/s,(n=0,1,2,3…).
| 1 |
| 4 |
| 4△t |
| 4n+1 |
v=
| λ |
| T |
| λ | ||
|
| λ |
| 4△t |
| 8 |
| 4×2 |
同理,若波沿x轴负方向传播:△t=(n+
| 3 |
| 4 |
| λ |
| T |
解得:v=(4n+3)m/s,(n=0,1,2,3…)
答:若波沿x轴正方向传播这列波的波速为(4n+1)m/s,(n=0,1,2,3…),若波沿x轴负方向传播这列波的波速为(4n+3)m/s,(n=0,1,2,3…).
点评:本题是知道两个时刻的波形研究波传播的距离、波速、周期的问题,关键是理解波的周期性,运用数学知识列出通项式.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
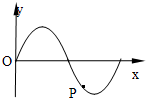 (2010?安徽)一列沿x轴方向传播的简谐横波,某时刻的波形如图所示.P为介质中的一个质点,从该时刻开始的一段极短时间内,P的速度v和加速度a的大小变化情况是( )
(2010?安徽)一列沿x轴方向传播的简谐横波,某时刻的波形如图所示.P为介质中的一个质点,从该时刻开始的一段极短时间内,P的速度v和加速度a的大小变化情况是( )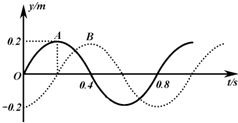 一列沿x轴方向传播的简谐波,处在x1=4m和x2=16m的两质点A、B的振动图象如图实线和虚线所示,已知该波的波长大于12m,由此可知( )
一列沿x轴方向传播的简谐波,处在x1=4m和x2=16m的两质点A、B的振动图象如图实线和虚线所示,已知该波的波长大于12m,由此可知( )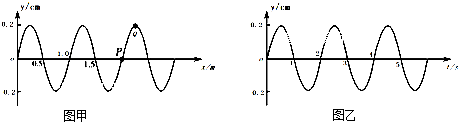
 (2008?崇文区一模)一列沿x轴方向传播的简谐横波,t=0时刻的波形如图中实线所示,t=0.2s时刻的波形为如图虚线所示,则( )
(2008?崇文区一模)一列沿x轴方向传播的简谐横波,t=0时刻的波形如图中实线所示,t=0.2s时刻的波形为如图虚线所示,则( )