题目内容
如图所示，长为L的平板小车C静止在光滑水平面上，现有A、B两个小物体（可视为质点）分别从小车C的左、右两端同时水平地滑上小车，初速度VA=V0，VB=3V0，两物体与小车间的动摩擦因数相同，三物体的质量之比mA︰mB︰mC=1︰1︰2,最后两物体恰好相遇而未碰撞，且与小车C相对静止，若重力加速度为g.求：
（1）两物体与小车间的动摩擦因数µ.
（2）A物体相对于地面向右运动的最大位移SA.
 |
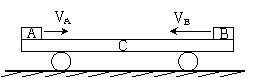（1）设A物体的质量为m，A、B、C组成的系统，设其最终的共同速度为v，则由题意，根据动量守恒定律有:
mvB－mvA=4mv （4分） 解得 v=
v0 （1分）
设A、B物体相对于C的位移分别为S1、S2，则由题意，根据能的转化和守恒定律有:
μmgS1＋μmgS2＝mvA2+mvB2－×4mv2 （4分）
而S1+S2=L （1分） 解得 μ＝
（2分）
（2）当A物体对地面的速度为零时，其向右运动的位移最大，对A物体，根据动能定理有:
－μmgSA=0－mvA2 （4分） 解得SA＝
（2分）
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
（2012?宝山区二模）如图所示，长为L的直棒一端可绕固定轴O转动，另一端搁在升降平台上，平台以速度v匀速上升，当棒与竖直方向的夹角为α时，棒的角速度为（ ）
（2005?潍坊模拟）如图所示，长为L的金属导线弯成一圆环，导线的两端接在电容为C的平行板电容器上，P、Q为电容器的两个极板，磁场垂直环面向里，磁感应强度以B=B0+Kt（K＞0）随时间变化t=0时，P、Q两板电势不相等．两板间的距离远小于环的半径，经时间t电容器P板（ ）
如图所示，长为L的金属导线弯成一圆环，导线的两端接在电容为C的平行板电容器上，P、Q为电容器的两个极板，磁场垂直于环面向里，磁感应强度以B=B0+Kt（K＞0）随时间变化，t=0时，P、Q两板电势相等．两板间的距离远小于环的半径，经时间t，电容器P板带
为3mg的拉力时就会断裂．现让环与球一起以
的
．