题目内容
 如图所示,M、N为两块水平放置的平行金属板,距平行板右端L处有竖直屏,平行板长、板间距均为2L,板间电压恒定.一带电粒子(重力不计)以平行于板的初速度v0沿两板中线进入电场,粒子在屏上的落点距O点距离为L,当分布均匀的大量上述粒子均以平行于板的初速度v0从MN板左端各位置进入电场(忽略粒子间的相互作用),则( )
如图所示,M、N为两块水平放置的平行金属板,距平行板右端L处有竖直屏,平行板长、板间距均为2L,板间电压恒定.一带电粒子(重力不计)以平行于板的初速度v0沿两板中线进入电场,粒子在屏上的落点距O点距离为L,当分布均匀的大量上述粒子均以平行于板的初速度v0从MN板左端各位置进入电场(忽略粒子间的相互作用),则( )分析:假设所有的粒子通过电场后向上偏转,由三角形相似法求出粒子通过电场时偏转的距离y,由几何关系即可得到有多少粒子能到达屏上.根据推论粒子射出电场时速度的反向延长线通过水平位移的中点,由题知道粒子在屏上偏离距离Y=L
解答:解:假设所有的粒子通过电场后向上偏转,每个粒子通过电场时偏转距离都相同,设为y.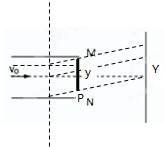
由题知,粒子在屏上偏离距离Y=L,由三角形相似法得
=
=
所以y=
Y=
L
由图可知,在MP范围内有粒子射出电场,MP=2L-
L=
L
则有
=
的粒子能够打到屏上,
故选:D.

由题知,粒子在屏上偏离距离Y=L,由三角形相似法得
| y |
| Y |
| L |
| L+L |
| 1 |
| 2 |
所以y=
| 1 |
| 2 |
| 1 |
| 2 |
由图可知,在MP范围内有粒子射出电场,MP=2L-
| 1 |
| 2 |
| 3 |
| 2 |
则有
| ||
| 2L |
| 3 |
| 4 |
故选:D.
点评:本题关键是利用几何知识求出偏转距离,再确定有多少粒子打到屏上.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 (2005?江苏)如图所示,M、N为两块带等量异种电荷的平行金属板,S1、S2为板上正对的小孔,N板右侧有两个宽度均为d的匀强磁场区域,磁感应强度大小均为B,方向分别垂直于纸面向外和向里,磁场区域右侧有一个荧光屏,取屏上与S1、S2共线的O点为原点,向上为正方向建立x轴.M板左侧电子枪发射出的热电子经小孔S1进入两板间,电子的质量为m,电荷量为e,初速度可以忽略.
(2005?江苏)如图所示,M、N为两块带等量异种电荷的平行金属板,S1、S2为板上正对的小孔,N板右侧有两个宽度均为d的匀强磁场区域,磁感应强度大小均为B,方向分别垂直于纸面向外和向里,磁场区域右侧有一个荧光屏,取屏上与S1、S2共线的O点为原点,向上为正方向建立x轴.M板左侧电子枪发射出的热电子经小孔S1进入两板间,电子的质量为m,电荷量为e,初速度可以忽略.
 (2009?湛江二模)如图所示,M、N为两对圆弧塑料导轨,分别粘接在U形金属导轨上层的C、D、E、F点,三导轨平滑连接且宽均为L=1m,导轨下层距离水平地面高为H=0.2m,在其上方放置一单向导电、质量为m2=1kg的金属杆2(已知金属杆2在P端电势高于Q端电势时有电流通过,反之无电流通过),整个装置放在竖直向上的 匀强磁场中,磁场的磁感应强度为B=0.1T.已知质量为m1=0.5kg的金属杆1在M轨道上从高为h=0.8m处由静止释放沿导轨M滑下,经U形金属导轨上层水平部分后滑上塑料导轨N,金属杆1与U形金属导轨上层水平部分接触良好,多次反复运动后使金属杆2脱离轨道着地,着地点到下层轨道右端水平距离为s=0.2m处,金属杆1和金属杆2导电时的电阻之和为R=2Ω(忽略一切摩擦和导轨的电阻),取g=10m/s2.求:
(2009?湛江二模)如图所示,M、N为两对圆弧塑料导轨,分别粘接在U形金属导轨上层的C、D、E、F点,三导轨平滑连接且宽均为L=1m,导轨下层距离水平地面高为H=0.2m,在其上方放置一单向导电、质量为m2=1kg的金属杆2(已知金属杆2在P端电势高于Q端电势时有电流通过,反之无电流通过),整个装置放在竖直向上的 匀强磁场中,磁场的磁感应强度为B=0.1T.已知质量为m1=0.5kg的金属杆1在M轨道上从高为h=0.8m处由静止释放沿导轨M滑下,经U形金属导轨上层水平部分后滑上塑料导轨N,金属杆1与U形金属导轨上层水平部分接触良好,多次反复运动后使金属杆2脱离轨道着地,着地点到下层轨道右端水平距离为s=0.2m处,金属杆1和金属杆2导电时的电阻之和为R=2Ω(忽略一切摩擦和导轨的电阻),取g=10m/s2.求: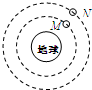 如图所示,M、N为两颗绕地球做匀速圆周运动的卫星,下列说法正确的是( )
如图所示,M、N为两颗绕地球做匀速圆周运动的卫星,下列说法正确的是( )