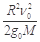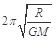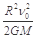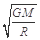题目内容
我国的“嫦娥一号”已于2007年10月24日以近乎完美的方式迈出了“准时发射,准确入轨,精密测控,精确变轨,成功绕月,成功探测”的关键六步.若已知月球质量为M,半径为R,万有引力恒量为G,月球表面重力加速度为g0,以下畅想可能的是( )
分析:1、由星球表面附近的重力等于万有引力求出星球表面重力加速度.对于荡秋千这种曲线运动求高度,我们应该运用机械能守恒定律或动能定理,求出上升的最大高度.
2、根据万有引力提供向心力G
=m
r=m
,得T=2π
,v=
,当r最小等于月球半径R时,周期最小为T=2π
,卫星发射得越高需要的发射速度越大,当发射到近月轨道,即r=R时,需要的发射速度最小,最小速度等于v=
.
2、根据万有引力提供向心力G
| Mm |
| r2 |
| 4π2 |
| T2 |
| v2 |
| r |
|
|
|
|
解答:解:A、C、由星球表面附近的重力等于万有引力,
即:
=mg星
则 g星=
经过最低位置向上的过程中,重力势能减小,动能增大.
由机械能守恒定律得:
mv02=mg星h
则能上升的最大高度h=
.故A错误、C正确.
B、根据万有引力提供向心力G
=m
r,得T=2π
,当r最小等于月球半径R时,周期最小为T=2π
,故B错误.
D、根据万有引力提供向心力G
=m
,得v=
,卫星发射得越高需要的发射速度越大,当发射到近月轨道,即r=R时,需要的发射速度最小,最小速度等于v=
,故D正确.
故选:CD.
即:
| GMm |
| R2 |
则 g星=
| GM |
| R2 |
经过最低位置向上的过程中,重力势能减小,动能增大.
由机械能守恒定律得:
| 1 |
| 2 |
则能上升的最大高度h=
| v02R2 |
| 2GM |
B、根据万有引力提供向心力G
| Mm |
| r2 |
| 4π2 |
| T2 |
|
|
D、根据万有引力提供向心力G
| Mm |
| r2 |
| v2 |
| r |
|
|
故选:CD.
点评:把星球表面的物体运动和天体运动结合起来是考试中常见的问题.重力加速度g是天体运动研究和天体表面宏观物体运动研究联系的物理量.

练习册系列答案
相关题目
我国的“嫦娥一号”已于2007年10月24日以近乎完美的方式迈出了“准时发射,准确入轨,精密测控,精确变轨,成功绕月,成功探测”的关键六步。若已知月球质量为M,半径为R,万有引力恒量为G,月球表面重力加速度为g0,以下畅想可能的是( )
A.在月球表面上荡秋千,将人视为质点,秋千质量不计、摆长不变,摆角小于90°,若秋千经过最低位置时的速度为ν0,则人能上升的最大高度是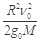 |
B.在月球上发射一颗绕它运行的卫星的最小周期为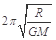 |
C.在月球表面以初速度ν0竖直上抛一个物体,物体上升的最大高度为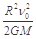 |
D.在月球上发射一颗绕它运动的卫星的最小发射速度为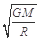 |