题目内容
4.“北斗第二代导航卫星网”将由5颗静止轨道卫星和30颗非静止轨道卫星组成,其中静止轨道卫星,是指高度为36000km的地球同步卫星;30颗非静止轨道卫星由27颗中轨(MEO)卫星和3颗倾斜同步(IGSO)卫星组成,其中27颗MEO卫星的轨道高度均为21500km,3颗倾斜同步(IGSO)卫星的轨道高度与静止轨道卫星的轨道高度相同,将各卫星轨道均视为圆轨道,根据以上信息,可以判断( )| A. | MEO卫星的角速度比静止轨道卫星的角速度小 | |
| B. | 该35颗卫星的轨道圆心可能不重合 | |
| C. | 静止轨道卫星只能在赤道正上方 | |
| D. | 静止轨道卫星和倾斜同步(IGSO)卫星的周期不相同 |
分析 根据万有引力提供向心力$G\frac{Mm}{{r}^{2}}=m{ω}^{2}r$=$m{(\frac{2π}{T})}^{2}r$,得到角速度、周期与轨道半径的关系,根据轨道高度的大小,比较角速度和周期的大小.
同步卫星的轨道为赤道上空36000km的高度,所有同步卫星都在同一个轨道上.
解答 解:A、根据万有引力提供向心力$G\frac{Mm}{{r}^{2}}=m{ω}^{2}r$,得$ω=\sqrt{\frac{GM}{{r}^{3}}}$,由此可知,轨道高度越大,角速度越小,MEO卫星的轨道高度为21500km,远小于静止轨道卫星36000km,故MEO卫星的角速度比静止轨道卫星的角速度大,故A错误.
B、卫星在运行的过程中,重力提供向心力,所以该35颗卫星的轨道圆心都是地球的球心,是重合的.故B错误;
C、同步卫星的轨道为赤道上空36000km的高度,所有同步卫星都在同一个轨道上,故C正确.
D、根据万有引力提供向心力$G\frac{Mm}{{r}^{2}}=m{(\frac{2π}{T})}^{2}r$,得$T=2π\sqrt{\frac{{r}^{3}}{GM}}$,轨道高度相同,周期相同,倾斜同步(IGSO)卫星的轨道高度与静止轨道卫星的轨道高度相同,故静止轨道卫星和倾斜同步(IGSO)卫星的周期相同,都是24h.故D错误.
故选:C.
点评 本题要掌握万有引力提供向心力,并且根据题意要能够用角速度和周期表示出向心力.要知道同步卫星的轨道为赤道上空36000km的高度,所有同步卫星都在同一个轨道上.

练习册系列答案
相关题目
15. 某军事试验场正在平地上试射地对空导弹,若某次竖直向上发射导弹时发生故障,造成导弹的v-t图象如图所示,则下述说法中正确的是( )
某军事试验场正在平地上试射地对空导弹,若某次竖直向上发射导弹时发生故障,造成导弹的v-t图象如图所示,则下述说法中正确的是( )
 某军事试验场正在平地上试射地对空导弹,若某次竖直向上发射导弹时发生故障,造成导弹的v-t图象如图所示,则下述说法中正确的是( )
某军事试验场正在平地上试射地对空导弹,若某次竖直向上发射导弹时发生故障,造成导弹的v-t图象如图所示,则下述说法中正确的是( )| A. | 0~1 s内导弹匀速上升 | B. | 1 s~2 s内导弹静止不动 | ||
| C. | 2 s~3 s内导弹匀速下落 | D. | 5 s末导弹恰好回到出发点 |
 如图所示,将边长为l、总电阻为R的正方形闭合线圈,从磁感强度为 B的匀强磁场中以速度v匀速拉出(磁场方向,垂直线圈平面)
如图所示,将边长为l、总电阻为R的正方形闭合线圈,从磁感强度为 B的匀强磁场中以速度v匀速拉出(磁场方向,垂直线圈平面)

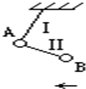
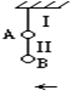
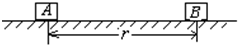 如图所示,绝缘水平面上静止着两个质量均为m、电荷量均为+Q的物体A和B(A、B均可视为质点),它们间的距离为r,与水平面间的动摩擦因数均为μ.求:
如图所示,绝缘水平面上静止着两个质量均为m、电荷量均为+Q的物体A和B(A、B均可视为质点),它们间的距离为r,与水平面间的动摩擦因数均为μ.求: 如图所示,在E=1×103V/m的竖直匀强电场中,有一光滑的半圆形绝缘轨QPN与一水平绝缘轨道MN连接,半圆形轨道平面与电场线平行,P为QN圆弧的中点,其半径R=40cm,一带正电q=10-4C的小滑块质量m=10g,位于N点右侧s=1.5m处,与水平轨道间的动摩擦因数μ=0.15,取g=10m/s2.现给小滑块一向左的初速度,滑块恰能运动到圆轨道的最高点Q,求:
如图所示,在E=1×103V/m的竖直匀强电场中,有一光滑的半圆形绝缘轨QPN与一水平绝缘轨道MN连接,半圆形轨道平面与电场线平行,P为QN圆弧的中点,其半径R=40cm,一带正电q=10-4C的小滑块质量m=10g,位于N点右侧s=1.5m处,与水平轨道间的动摩擦因数μ=0.15,取g=10m/s2.现给小滑块一向左的初速度,滑块恰能运动到圆轨道的最高点Q,求: 如图所示,△ABC为一直角三棱镜的截面,其顶角θ=30°,P为垂直于直线BCD的光屏,现一宽度等于AB的单色平行光束垂直射向AB面,在屏P上形成一条宽度等于$\frac{2}{3}\overline{AB}$的光带,求棱镜的折射率.
如图所示,△ABC为一直角三棱镜的截面,其顶角θ=30°,P为垂直于直线BCD的光屏,现一宽度等于AB的单色平行光束垂直射向AB面,在屏P上形成一条宽度等于$\frac{2}{3}\overline{AB}$的光带,求棱镜的折射率. 如图所示,在xOy坐标系中,x轴上N点到O点的距离是12cm,虚线NP与x轴负向的夹角是30°.第Ⅰ象限内NP的上方有匀强磁场,磁感应强度B=1T,第IV象限有匀强电场,方向沿y轴正向.一质量m=8×10-10kg.电荷量q=1×10-4C 带正电粒子,从电场中M(12,-8)点由静止释放,经电场加速后从N点进入磁场,又从y轴上P点穿出磁场.不计粒子重力,取π=3.
如图所示,在xOy坐标系中,x轴上N点到O点的距离是12cm,虚线NP与x轴负向的夹角是30°.第Ⅰ象限内NP的上方有匀强磁场,磁感应强度B=1T,第IV象限有匀强电场,方向沿y轴正向.一质量m=8×10-10kg.电荷量q=1×10-4C 带正电粒子,从电场中M(12,-8)点由静止释放,经电场加速后从N点进入磁场,又从y轴上P点穿出磁场.不计粒子重力,取π=3.