题目内容
16.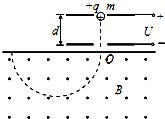 如图所示,两平行金属板间距为d,电势差为U,板间电场可视为匀强电场;金属板下方有一磁感应强度为B的匀强磁场.带电量为+q、质量为m的粒子,由静止开始从正极板出发,经电场加速后射出,并进入磁场做匀速圆周运动.忽略重力的影响,求:
如图所示,两平行金属板间距为d,电势差为U,板间电场可视为匀强电场;金属板下方有一磁感应强度为B的匀强磁场.带电量为+q、质量为m的粒子,由静止开始从正极板出发,经电场加速后射出,并进入磁场做匀速圆周运动.忽略重力的影响,求:(1)粒子从电场射出时速度v的大小;
(2)粒子在磁场中做匀速圆周运动的半径R.
分析 (1)根据动能定理求得粒子从电场射出时的速度大小;
(2)带电粒子进入磁场在洛伦兹力作用下做匀速圆周运动,根据洛伦兹力提供圆周运动向心力求得粒子圆周运动的半径.
解答 解:(1)设带电粒子射出电场时的速度为v,由动能定理可得:
$Uq=\frac{1}{2}m{v}^{2}-0$
解得粒子射出速度v=$\sqrt{\frac{2Uq}{m}}$
(2)带电粒子在磁场中做匀速圆周运动,由牛顿第二定律可得:
$qvB=m\frac{{v}^{2}}{R}$
可得带电粒子圆周运动的半径R=$\frac{mv}{qB}$=$\frac{m}{qB}\sqrt{\frac{2Uq}{m}}$=$\frac{1}{B}\sqrt{\frac{2mU}{q}}$
答:(1)粒子从电场中射出时的速度为$\sqrt{\frac{2Uq}{m}}$;
(2)粒子在磁场中做匀速圆周运动的半径为$\frac{1}{B}\sqrt{\frac{2mU}{q}}$.
点评 带电粒子在电场中加速可以根据动能定理求解加速的速度,在磁场中做匀速圆周运动根据洛伦兹力提供圆周运动向心力列式求解是关键.

练习册系列答案
相关题目
8. 如图所示,理想变压器输入端PQ接电压一定的交流电源,通过单刀双掷开关S可改变变压器原线圈匝数,电压表及电流表皆为理想电表,则下列说法中正确的是( )
如图所示,理想变压器输入端PQ接电压一定的交流电源,通过单刀双掷开关S可改变变压器原线圈匝数,电压表及电流表皆为理想电表,则下列说法中正确的是( )
 如图所示,理想变压器输入端PQ接电压一定的交流电源,通过单刀双掷开关S可改变变压器原线圈匝数,电压表及电流表皆为理想电表,则下列说法中正确的是( )
如图所示,理想变压器输入端PQ接电压一定的交流电源,通过单刀双掷开关S可改变变压器原线圈匝数,电压表及电流表皆为理想电表,则下列说法中正确的是( )| A. | 当滑片c向b端移动时,变压器的输入功率不变 | |
| B. | 当滑片c向b端移动时,电流表A1的示数将变大 | |
| C. | 当滑片c向a端移动时,电压表V的示数将不变 | |
| D. | 将开关S由1掷向2时,三个电表的示数都变大 |
6.下列关于力的叙述中,正确的是( )
| A. | 力是使物体位移增加的原因 | |
| B. | 力是维持物体运动速度的原因 | |
| C. | 合力的大小可能比一个分力大,而比另一个分力小 | |
| D. | 力是使物体产生加速度的原因 |
 在练习使用多用电表的实验中:
在练习使用多用电表的实验中:



 如图甲为利用气垫导轨(滑块在该导轨上运动时所受阻力可忽略)“验证机械能守恒定律”的实验装置,请结合以下实验步骤完成填空.
如图甲为利用气垫导轨(滑块在该导轨上运动时所受阻力可忽略)“验证机械能守恒定律”的实验装置,请结合以下实验步骤完成填空. 如图所示,有一原长x=0.5m、劲度系数k=100N/m的轻质弹簧穿过一光滑金属杆,弹簧一端固定在金属杆的一端点O,另一端与穿过金属杆的小球相连,小球质量m=1kg,整个装置在竖直平面内绕O点转动.取g=10m/s2,$\sqrt{13}$=3.6,$\sqrt{5}$=2.24.
如图所示,有一原长x=0.5m、劲度系数k=100N/m的轻质弹簧穿过一光滑金属杆,弹簧一端固定在金属杆的一端点O,另一端与穿过金属杆的小球相连,小球质量m=1kg,整个装置在竖直平面内绕O点转动.取g=10m/s2,$\sqrt{13}$=3.6,$\sqrt{5}$=2.24. 一轻绳(足够长)跨过两个等高的轻定滑轮(不计大小和摩擦),两端分别挂上物体A、B,其中物体A的质量m1=6kg,物体B的质量m2=5kg,如图所示,在滑轮之间的绳上O点拴接另一段轻绳悬挂住质量为朋的物体C,使三个物体均保持静止状态,其中OP段绳子与竖直方向夹角为α=30°,OQ段绳子与竖直方向夹角为β,求:
一轻绳(足够长)跨过两个等高的轻定滑轮(不计大小和摩擦),两端分别挂上物体A、B,其中物体A的质量m1=6kg,物体B的质量m2=5kg,如图所示,在滑轮之间的绳上O点拴接另一段轻绳悬挂住质量为朋的物体C,使三个物体均保持静止状态,其中OP段绳子与竖直方向夹角为α=30°,OQ段绳子与竖直方向夹角为β,求: