题目内容
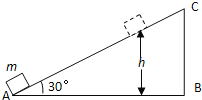
【题目】如图所示，竖直平面内的轨道ABCD由水平部分AB与光滑的四分之一圆弧轨道CD组成，AB恰与圆弧CD在C点相切，其总质量M=4 kg，其右侧紧靠在固定挡板上，静止在光滑水平面上。在轨道的左端有一质量为m=1 kg的小滑块（可视为质点）以v0=3 m/s的速度向右运动，小滑块刚好能冲到D点。已知小滑块与长木板AB间的动摩擦因数
=0.5，轨道水平部分AB的长度L=0.5 m，g取10 m/s2。求：
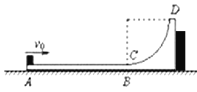
（1）小滑块经过C点时对轨道的压力大小；
（2）轨道ABCD的最终速度大小。
【答案】（1）30N（2）0.4m/s
【解析】(1)对小滑块，从A到B过程中，
由动能定理得：
，解得：
从C到D中，由动能定理得：
解得
在C点有：
，解得：
（2）物块从D重新回到C过程有：
，解得：
滑块再次滑上木板时，若木板长度足够，则最终两者相对静止，此过程对滑块木板系统动量守恒有：
，解得：v=0.4m/s
根据能量守恒：
由以上两式可求得：
因为
，故物体未能从木板上滑下。
轨道的最终速度v=0.4m/s
【题目】某实验小组探究弹簧的劲度系数k与其长度（圈数）的关系；实验装置如图（a）所示：一均匀长弹簧竖直悬挂，7个指针P0、P1、P2、P3、P4、P5、P6分别固定在弹簧上距悬点0、10、20、30、40、50、60圈处；通过旁边竖直放置的刻度尺，可以读出指针的位置，P0指向0刻度；设弹簧下端未挂重物时，各指针的位置记为x0；挂有质量为0.100kg砝码时，各指针的位置记为x；测量结果及部分计算结果如下表所示（n为弹簧的圈数，取重力加速度为9.80m/s2）.已知实验所用弹簧的总圈数为60，整个弹簧的自由长度为11.88cm.
P1 | P2 | P3 | P4 | P5 | P6 | |
x0 （cm） | 2.04 | 4.06 | 6.06 | 8.05 | 10.03 | 12.01 |
x（cm） | 2.64 | 5.26 | 7.81 | 10.30 | 12.93 | 15.41 |
n | 10 | 20 | 30 | 40 | 50 | 60 |
k（N/m） | 163 | ① | 56.0 | 43.6 | 33.8 | 28.8 |
1/k（m/N） | 0.0061 | ② | 0.0179 | 0.0229 | 0.0296 | 0.0347 |
（1）将表中数据补充完整：______，________；
（2）以n为横坐标，1/k为纵坐标，在图（b）给出的坐标纸上画出1/k-n图象______；
（3）图（b）中画出的直线可以近似认为通过原点；若从实验中所用的弹簧截取圈数为n的一段弹簧，该弹簧的劲度系数k与其圈数n的关系的表达式为k=_______N/m；该弹簧的劲度系数k与其自由长度l0（单位为m）的表达式为k=______N/m.
