Question

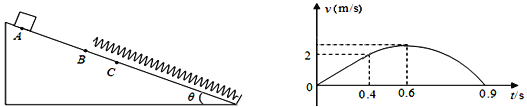
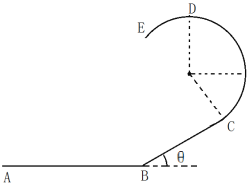
【题目】如图所示，某同学搭建的轨道，CDE为半径R=0.3m的光滑圆弧型轨道，C点与斜面BC相切，D点为轨道最高点，斜面倾角θ=30°，与水平轨道AB相交点B点附近用一段小圆弧平滑连接。该同学用一辆质量m=0.2kg的玩具小车从A点由静止开始出发，先作匀加速直线运动到达B点时恰好达到额定功率，匀加速时间t=1s，此后再以恒定功率行驶到C点关闭玩具车电动机。已知玩具车在AB段受到恒定阻力f=0.2N，BC段、CDE段都不受阻力，AB段长为2m，BC段长为1.3m。试求：

(1)玩具车在AB段的牵引力及额定功率P；

(2)判断玩具车能否运动到D点。若能，则求一下对D点的压力；若不能则说明理由；

(3)若小车行驶到B点时，突然出现了故障，额定功率降为3W，发现玩具车到达C点前已经匀速，则求玩具车在BC段行驶的时间。

Answer 1

【答案】(1)，；(2)能过D点，；(3)

【解析】

(1)汽车在AB段做匀加速直线运动，有

联立可得

玩具车到达B点时恰好达到额定功率，有

(2)玩具车在BC段保持功率恒定，准备爬坡时牵引力为，而不受阻力，重力的分力为

故在BC段玩具车做匀速直线运动，C点的速度为4m/s，假设玩具车能经过最高点D点，由动能定理有

解得

若要安全过D点的最小速度满足只有重力提供向心力，有

则可得

故，可知玩具车能安全通过最高点D，由牛顿第二定律有

由牛顿第三定律有

联立可得玩具车对D点的压力为。

(3)玩具车从B点到C点保持功率为不变，设运动时间为，匀速的速度为，有

联立可得