题目内容
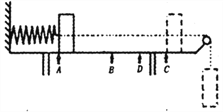
【题目】如图所示,水平放置的平行板电容器极板中央开有一小圆孔,两极板间距d1 =0.4m,极板M、N间的电势差U1=400V;紧靠N极板的下方有一竖直放置的平行板电容器PQ,极板P、Q间电势差为U2。一带正电小球从靠近M极板中心位置的O点静止释放,小球竖直向下运动穿过N极板中央小孔,并从P、Q两板上端连线的中点进入P、Q极板间做曲线运动。已知小球的质量m =5×10-6kg,电荷量q=5×10-8 C,重力加速度g=10m/s2。

(1)求小球穿过N极板中央小孔时的速度![]() ;
;
(2)若小球能从电容器PQ下端飞出,求两极板P、Q间电势差U2的取值范围。
【答案】(1)4m/s(2)-400V≤U2≤400V
【解析】(1)带电小球从极板M到极板N的运动过程中,由动能定理: ![]()
解得小球穿过N极板中央小孔时的速度: ![]()
(2)小球进入电容器PQ极板间运动时,在竖直方向上做初速度v0,加速度为g的匀加速运动,当从极板下端飞出时,竖直位移为l,由位移公式可得: ![]()
可得小球在PQ极板运动的时间:t=0.1s
设电容器PQ两极板间的电势差最大值为U,小球进入电容器 PQ极板间运动时,在水平方向上做初速度为0的匀加速运动,由牛顿第二定律可得: ![]()
当极板间的电势差最大时,小球应从极板的下端点飞出,其水平位移为d2/2,则: ![]()
由以上三式联立可得电容器PQ两板间的电势差的最大值为:U=400V
小球能从电容器PQ下端飞出,PQ两板间的电势差的取值范围为:-400V≤U2≤400V

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目