题目内容
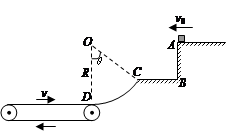
如图所示,半径为R的3/4圆周轨道固定在竖直平面内,O为圆轨道的圆心,D为圆轨道的最高点,圆轨道内壁光滑,圆轨道右侧的水平面BC与圆心等高。质量为m的小球从离B点高度为h处的A点由静止开始下落,从B点进入圆轨道,小球能通过圆轨道的最高点,并且在最高点对轨道的额压力不超过3mg。现由物理知识推知,小球下落高度h与圆轨道半径R及小球经过D点时的速度vD之间的关系为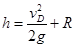 。
。
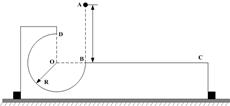
(1)求高度h应满足的条件;
(2)通过计算说明小球从D点飞出后能否落在水平面BC上,并求落点与B点水平距离的范围。
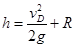 。
。
(1)求高度h应满足的条件;
(2)通过计算说明小球从D点飞出后能否落在水平面BC上,并求落点与B点水平距离的范围。
(1) (2)
(2)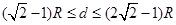
 (2)
(2)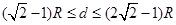
试题分析:(1)当小球刚好通过最高点时重力提供向心力,则应有:

解得

由题设条件可得此时对应的AB间高度h为
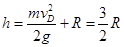
(2)由(1)知在最高点D速度至少为
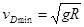
此时飞离D后平抛,有:
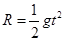 ,
,
联立解得
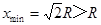
故能落在水平面BC上。
当小球在最高点对轨道的压力为3mg时有
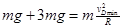
解得
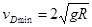
飞离D后平抛
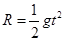 ,
,
联立解得
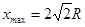
故落点与B点水平距离的范围为
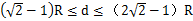

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目