题目内容
9. 如图所示,质量分别为M,m的两物块A,B叠放在一起沿光滑水平地面以速度v做匀速直线运动,A,B间的动摩擦因数为μ.在t=0时刻对物体A施加一个随着时间变化的推力F=kt,k为一常量,则从力F作用开始,在物块刚要发生相对滑动所经过的时间为$\frac{μMg(M+m)}{mk}$.
如图所示,质量分别为M,m的两物块A,B叠放在一起沿光滑水平地面以速度v做匀速直线运动,A,B间的动摩擦因数为μ.在t=0时刻对物体A施加一个随着时间变化的推力F=kt,k为一常量,则从力F作用开始,在物块刚要发生相对滑动所经过的时间为$\frac{μMg(M+m)}{mk}$.
分析 根据A、B间的最大静摩擦力,隔离对B分析,求出最大加速度,再对整体分析,求出最大推力,从而得出经历的时间.
解答 解:当A、B间摩擦力达到最大时,大小f=μMg,
隔离对B分析,最大加速度$a=\frac{f}{m}=\frac{μMg}{m}$,
对整体分析,F=(M+m)a=kt,
解得t=$\frac{μMg(M+m)}{mk}$.
故答案为:$\frac{μMg(M+m)}{mk}$.
点评 本题考查了牛顿第二定律临界问题,抓住临界状态,通过整体法和隔离法求出最大加速度是关键.

练习册系列答案
相关题目
19. 如图,两根光滑金属导轨平行放置,导轨所在平面与水平面间的夹角为θ,整个装置处于垂直于导轨平面方向的匀强磁场中.质量为m的金属杆ab垂直导轨放置,当杆中通从a 到b的电流I时,ab刚好静止.则( )
如图,两根光滑金属导轨平行放置,导轨所在平面与水平面间的夹角为θ,整个装置处于垂直于导轨平面方向的匀强磁场中.质量为m的金属杆ab垂直导轨放置,当杆中通从a 到b的电流I时,ab刚好静止.则( )
 如图,两根光滑金属导轨平行放置,导轨所在平面与水平面间的夹角为θ,整个装置处于垂直于导轨平面方向的匀强磁场中.质量为m的金属杆ab垂直导轨放置,当杆中通从a 到b的电流I时,ab刚好静止.则( )
如图,两根光滑金属导轨平行放置,导轨所在平面与水平面间的夹角为θ,整个装置处于垂直于导轨平面方向的匀强磁场中.质量为m的金属杆ab垂直导轨放置,当杆中通从a 到b的电流I时,ab刚好静止.则( )| A. | 磁场方向垂直于导轨平面向下 | B. | 磁场方向垂直于导轨平面向上 | ||
| C. | ab受安培力的大小等于mgsinθ | D. | ab受安培力的大小等于mgtanθ |
17.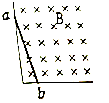 如图所示,金属杆a端靠在竖直导电轨道上,b端位于水平导电轨道上,金属杆与轨道接触良好,形成闭合回路.水平方向的匀强磁场与闭合电路平面垂直,使金属杆由图示位置沿轨道滑到水平位置,在滑动过程中a、b两端始终保持与导轨良好接触.这段过程中,a、b两点的电势φa、φb的大小相比较是( )
如图所示,金属杆a端靠在竖直导电轨道上,b端位于水平导电轨道上,金属杆与轨道接触良好,形成闭合回路.水平方向的匀强磁场与闭合电路平面垂直,使金属杆由图示位置沿轨道滑到水平位置,在滑动过程中a、b两端始终保持与导轨良好接触.这段过程中,a、b两点的电势φa、φb的大小相比较是( )
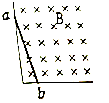 如图所示,金属杆a端靠在竖直导电轨道上,b端位于水平导电轨道上,金属杆与轨道接触良好,形成闭合回路.水平方向的匀强磁场与闭合电路平面垂直,使金属杆由图示位置沿轨道滑到水平位置,在滑动过程中a、b两端始终保持与导轨良好接触.这段过程中,a、b两点的电势φa、φb的大小相比较是( )
如图所示,金属杆a端靠在竖直导电轨道上,b端位于水平导电轨道上,金属杆与轨道接触良好,形成闭合回路.水平方向的匀强磁场与闭合电路平面垂直,使金属杆由图示位置沿轨道滑到水平位置,在滑动过程中a、b两端始终保持与导轨良好接触.这段过程中,a、b两点的电势φa、φb的大小相比较是( )| A. | φa>φb | B. | φa<φb | ||
| C. | 先是φa>φb,后是φa<φb | D. | 先是φa<φb后是φa>φb |
4.纸带上已按要求选出0,1,2,3,4,5,6七个计数点,相邻计数点间的距离一次为x1、x2、x3、x4、x5、x6,则可以判断和计算出( )
| A. | 计数点0对应速度v0一定为0 | |
| B. | 根据v1=$\frac{{x}_{1}+{x}_{2}}{2T}$可计算一号点的对应速度,同理可算出v2,v3,v4,v5 | |
| C. | 无法计算出v0和v6的大小 | |
| D. | 可作出v-t图象求出斜率即加速度 |
5.关于多普勒效应的叙述,下列说法不正确的是( )
| A. | 产生多普勒效应的原因是波源频率发生了变化 | |
| B. | 产生多普勒效应的原因是观察者和波源之间发生了相对运动 | |
| C. | 甲乙两列车相向行驶,两车均鸣笛,且所发生的笛声频率相同,乙车中的某旅客听到甲车笛声频率高于他所听到的乙车笛声频率 | |
| D. | 哈勃太空望远镜发现所接收到的来自于某一遥远星系上辐射的电磁波波长变长(称为哈勃红移),这说明该星系正在远离我们而去 |
3. 如图所示,从倾角为θ的斜面顶点A将一小球以初速度v0水平抛出,小球落在斜面上B点,重力加速度为g.(不计空气阻力)则下列说法正确的有( )
如图所示,从倾角为θ的斜面顶点A将一小球以初速度v0水平抛出,小球落在斜面上B点,重力加速度为g.(不计空气阻力)则下列说法正确的有( )
 如图所示,从倾角为θ的斜面顶点A将一小球以初速度v0水平抛出,小球落在斜面上B点,重力加速度为g.(不计空气阻力)则下列说法正确的有( )
如图所示,从倾角为θ的斜面顶点A将一小球以初速度v0水平抛出,小球落在斜面上B点,重力加速度为g.(不计空气阻力)则下列说法正确的有( )| A. | 从A到B的运动时间为 t=$\frac{4{v}_{0}tanθ}{g}$ | |
| B. | AB的长度为 L=$\frac{2{{v}_{0}}^{2}tanθ}{gcosθ}$ | |
| C. | 到B点的速度vB=v0$\sqrt{1+4ta{n}^{2}θ}$ | |
| D. | 小球在B点时的速度分量满足$\frac{{v}_{y}}{{v}_{x}}$=tanθ |
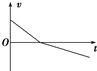
 如图所示,一质量为m的滑块,以初速度v0从倾角为θ的斜面底端滑上斜面,当其速度减为零后又沿斜面返回底端.已知滑块与斜面间的动摩擦因数为μ,若滑块所受的摩擦力为f、所受的合外力为F合、加速度为a、速度为v,选沿斜面向上为正方向,在滑块沿斜面运动的整个过程中,这些物理量随时间变化的图象大致正确的是( )
如图所示,一质量为m的滑块,以初速度v0从倾角为θ的斜面底端滑上斜面,当其速度减为零后又沿斜面返回底端.已知滑块与斜面间的动摩擦因数为μ,若滑块所受的摩擦力为f、所受的合外力为F合、加速度为a、速度为v,选沿斜面向上为正方向,在滑块沿斜面运动的整个过程中,这些物理量随时间变化的图象大致正确的是( )


 如图所示,一个边长L=10cm,匝数N=100匝的正方形线圈abcd在匀强磁场中绕垂直于磁感线的对称轴OO′匀速转动,磁感应强度B=0.50T,角速度ω=10π rad/s,外电路电阻R=4.0Ω,线圈内阻r=1.0Ω.
如图所示,一个边长L=10cm,匝数N=100匝的正方形线圈abcd在匀强磁场中绕垂直于磁感线的对称轴OO′匀速转动,磁感应强度B=0.50T,角速度ω=10π rad/s,外电路电阻R=4.0Ω,线圈内阻r=1.0Ω.