题目内容
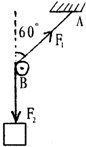
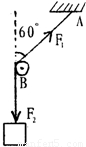
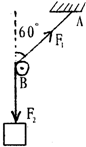如图所示，绳子上端固定于A，下端挂一重120N的重物，B是光滑的木栓，则F1和F2的大小分别为120
120
N，120
120
N．因此木栓B所受的绳子对它的压力为120
120
N，方向和竖直方向所成夹角为60°
60°
．分析：同一根绳子张力处处相等，木栓B所受的绳子对它的压力为F1和F2的合力，根据平行四边形定则求解其大小和方向．
解答：解：同一根绳子张力处处相等，故：F1=F2=G=120N；
木栓B所受的绳子对它的压力为F1和F2的合力，根据平行四边形定则作图如下：
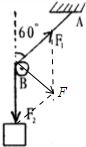
故压力等于120N，与竖直方向所成夹角为60°．
故答案为：120，120，120N，60°．
木栓B所受的绳子对它的压力为F1和F2的合力，根据平行四边形定则作图如下：
故压力等于120N，与竖直方向所成夹角为60°．
故答案为：120，120，120N，60°．
点评：本题是平行四边形定则的直接运用问题，关键明确同一根绳子的张力处处相等，基础题．
练习册系列答案
相关题目
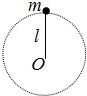如图所示，长l=0.5m，质量可忽略的细绳，其下端固定于O点，上端连有质量m=2kg的小球，它绕O点在竖直平面内做圆周运动，取g=10m/s2，当它恰好通过最高点时最高点的速率为
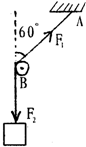如图所示，绳子上端固定于A，下端挂一重120N的重物，B是光滑的木栓，则F1和F2的大小分别为________N，________N．因此木栓B所受的绳子对它的压力为________N，方向和竖直方向所成夹角为________．
