��Ŀ����
����Ŀ����ͼ�����̶��ľ�Եб����Ǿ�Ϊ����������������ϸ������ab�������a�ˣ���cd�������c�ˣ����Ⱦ�ΪL�������ֱ�Ϊ2m��m�������������쳤���������߽��������ɱպϻ�·abdca����ͨ���̶���б�����ص����⻬��ԵС�����ֿ����б���ϣ�ʹ��������ˮƽ����б���ϴ�����ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB������ֱ��б�����ϡ���֪�������߸պò��ڴų��У���·����ΪR������������б���Ķ�Ħ��������Ϊ�����������ٶȴ�СΪg����֪������ab�����»�����
(1)�ж�ab���еĵ�������
(2)��a��b��������ab����ƽ����������ͼ��
(3)�����ڽ�����ab�ϵİ������Ĵ�С��
(4)�������˶��ٶȵĴ�С��

���𰸡�(1) ��ֱֽ�����⣻(2)ͼ��������(3) mg��sin��-3��cos������(4)![]()
��������
(1)�����ֶ����֪��ab���еĵ�������ֱֽ�����⣻
(2)����ab������ͼ��
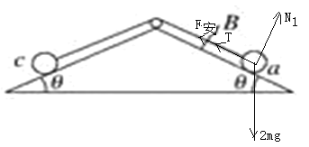
(3)�赼�ߵ������Ĵ�СΪT����б���ab����֧�����Ĵ�СΪN1��������ab���ϵİ������Ĵ�СΪF������б���cd��֧������СΪN2������ab����������ƽ��������
2mgsin������N1+T+F����
N1��2mgcos����
����cd����ͬ����
mgsin��+��N2��T��
N2��mgcos����
�����٢ڢۢ�ʽ��
F��=mg��sin��-3��cos������
(4)�ɰ�������ʽ��
F��=BIL��
����I��abcda�еĸ�Ӧ������ab���ϵĸ�Ӧ�綯��Ϊ
E=BLv��
ʽ�У�v��ab���»��ٶȵĴ�С����ŷķ���ɵ�
![]() ��
��
�����ݢޢߢ�ʽ��
![]() ��
��