题目内容
如图所示，AB为水平轨道，A、B间距离s＝2.25 m，BCD是半径为R＝0.40 m的竖直半圆形轨道，B为两轨道的连接点，D为轨道的最高点．一小物块质量为m＝1.2 kg，它与水平轨道和半圆形轨道间的动摩擦因数均为μ＝0.20．小物块在F＝12 N的水平力作用下从A点由静止开始运动，到达B点时撤去力F，小物块刚好能到达D点，g取10 m/s2，试求：
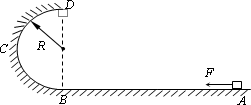
(1)撤去F时小物块的速度大小；
(2)在半圆形轨道上小物块克服摩擦力做的功；
(3)若半圆形轨道是光滑的，其他条件不变，求当小物块到达D点时对轨道的压力大小．
答案：
解析：
解析：
|
(1)以m为研究对象，受力情况如图所示：设物体在恒力作用下的加速度为a，小物块到达B点时的速度为vB 根据牛顿运动定律：F－μmg＝ma (2)设小物块到达D点时的速度为vD，又因为小物块恰能到达D点 所以 设重力和摩擦力所做的功分别为WG和Wf，由动能定理 所以在圆形轨道上小物块克服摩擦力做的功为Wf＝9.6 J (5分) (3)设圆轨道光滑时，小物块到达D点时的速度为 设小物块在D受到圆轨道的压力为N，所以： N＝48 N (5分) |
m/s (4分)
，由机械能守恒定律：
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
如图所示，AB为水平轨道，A、B间距离s=1m，BCD是半径为R=0.2m的竖直半圆形轨道，B为两轨道的连接点，D为轨道的最高点，整个轨道处于竖直向下的匀强电场中，场强大小为E=103N/C．一带正电q=5×10-3C的小物块质量为m=0.5kg，它与水平轨道间的动摩擦因数均为μ=0.1．小物块在F=10N的水平恒力作用下从A点由静止开始运动，到达B点时撤去力F，小物块刚好能到达D点，试求：（g=10m/s2）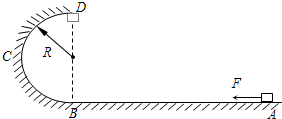
如图所示，AB为水平轨道，A、B间距离s=2.25m，BCD是半径为R=0.40m的竖直半圆形轨道，B为两轨道的连接点，D为轨道的最高点．一小物块质量为m=1.2kg，它与水平轨道和半圆形轨道间的动摩擦因数均为μ=0.20．小物块在F=12N的水平力作用下从A点由静止开始运动，到达B点时撤去力F，小物块刚好能到达D点，g取10m/s2，试求：
（2013?东城区二模）如图所示，AB为水平轨道，A、B间距离s=1.25m，BCD是半径为R=0.40m的竖直半圆形轨道，B为两轨道的连接点，D为轨道的最高点．有一小物块质量为m=1.0kg，小物块在F=10N的水平力作用下从A点由静止开始运动，到达B点时撤去力F，它与水平轨道和半圆形轨道间的摩擦均不计．g取10m/s2，求：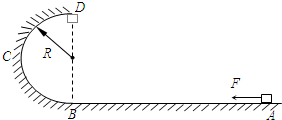
如图所示，AB为水平轨道，A、B间距离s=2.25m，BCD是半径为R=0.40m的竖直半圆形轨道，B为两轨道的连接点，D为轨道的最高点．一小物块质量为m=1.2kg，它与水平轨道和半圆形轨道间的动摩擦因数均为μ=0.20．小物块在F=12N的水平力作用下从A点由静止开始运动，到达B点时撤去力F，小物块刚好能到达D点，g取10m/s2，试求：
。一带正电
的小物块质量为m=0.5kg，它与水平轨道间的动摩擦因数均为μ=0.1。小物块在F=10N的水平恒力作用下从A点由静止开始运动，到达B点时撤去力F，小物块刚好能到达D点，试求：(g=10m/s2)