题目内容
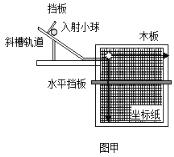
【题目】如图所示为车站使用的水平传送带的模型，皮带轮的半径均为R=0.1m，两轮轴距为L=3m，在电机的驱动下顺时针转动，现将一个旅行包（可视为质点）无初速放在水平传送带左端，已知旅行包与传送带之间的动摩擦因数为μ=0.6，g=10m/s2，不计空气阻力。
（1）要使旅行包到达右端不会直接飞出，传送带的速度应小于多少？
（2）若传送带实际速度为0.2m/s，春运期间每天传送的旅行包平均总质量为10吨，则电机每天相对于空载多消耗的电能E是多少？（所有旅行包均无初速，且与传送带间的μ相同）
【答案】（1）小于1m/s；（2）400J。
【解析】
（1）设旅行包从右端飞出的速度为v，受到传送带的支持力为FN，则由牛顿第二定律得：mg-FN=m
解得：v=
当FN=0时，v有最大值vmax=
=1m/s
旅行包一直加速能达到的最大速度为v′max=
=6m/s＞1m/s
故传送带的速度应小于1m/s
（2）旅行包在传送带上相对滑动过程中，传送带与旅行包对地位移分为别为：x传=v传t，
x包=
t
表示旅行包在滑动过程中的平均速度，有=
故有：x传=2x包
消耗电能为E=μmgx传
旅行包在滑动过程中动能的增量为：△Ek=μmgx包
故E=2△Ek
结论：电机对每一个旅行包多消耗的电能均为旅行包堵加动能的两倍，一半电能转化为动能，一半电能
转化为内能
故春运期每天多消耗的电能为10吨行包在传送带上获得总动能的两倍
E电=2△EK总=m总v02=10000×004J=400J
练习册系列答案
相关题目
