题目内容
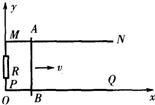 足够长且电阻不计的金属光滑导轨MN、PQ水平放置,导轨间距为d,M、P两点间接有阻值为R的电阻,建立平面直角坐标系,坐标轴x,y分别与PQ、PM重合,如图所示.空间存在垂直导轨平面且范围足够大的磁场,磁场沿x轴的分布规律为B=B0sin(
足够长且电阻不计的金属光滑导轨MN、PQ水平放置,导轨间距为d,M、P两点间接有阻值为R的电阻,建立平面直角坐标系,坐标轴x,y分别与PQ、PM重合,如图所示.空间存在垂直导轨平面且范围足够大的磁场,磁场沿x轴的分布规律为B=B0sin(| 2π | λ |
(1)导体棒运动到哪些位置,回路中的电流达到最大值;
(2)外力随时间t的变化关系;
(3)导体棒发生上个λ的位移过程中,电阻R上产生的焦耳热.
分析:(1)导体棒匀速运动切割磁感线产生的感应电动势E=Bdv,由欧姆定律I=
可得到电流的表达式,即可求得电流达到最大值时的位置.
(2)棒所受的安培力 F安=BId,因导体棒做匀速运动,外力与安培力平衡,可求得外力的表达式.
(3)当导体棒发生上个λ的位移过程中,交流电变化了一个周期,产生的焦耳热由焦耳定律求出,要注意用电流的有效值求解.
| E |
| R |
(2)棒所受的安培力 F安=BId,因导体棒做匀速运动,外力与安培力平衡,可求得外力的表达式.
(3)当导体棒发生上个λ的位移过程中,交流电变化了一个周期,产生的焦耳热由焦耳定律求出,要注意用电流的有效值求解.
解答:解:(1)导体棒切割磁感线产生的感应电动势为E=Bdv
感应电流为 I=
=
=
则知 电流最大时导体棒的位置坐标为 x=
λ(n=1,2,3…).
(2)导体棒所受的安培力 F安=BId
导体棒做匀速运动,外力与安培力平衡,则有 F=F安=BId
又 x=vt
联立得 F=
sin2(
vt)
(3)由I=
B0sin
vt,可知该交流电为正弦交流电,则在导体棒发生一个λ的位移过程中,交流电变化了一个周期.产生的焦耳热为:
Q=[
]2R?
=
答:
(1)导体棒运动到位置坐标为 x=
λ(n=1,2,3…)时,回路中的电流达到最大值;
(2)外力随时间t的变化关系为F=
sin2(
vt).
(3)导体棒发生上个λ的位移过程中,电阻R上产生的焦耳热是
.
感应电流为 I=
| E |
| R |
| Bdv |
| R |
B0dvsin(
| ||
| R |
则知 电流最大时导体棒的位置坐标为 x=
| 2n-1 |
| 4 |
(2)导体棒所受的安培力 F安=BId
导体棒做匀速运动,外力与安培力平衡,则有 F=F安=BId
又 x=vt
联立得 F=
| vd2 |
| R |
| B | 2 0 |
| 2π |
| λ |
(3)由I=
| dv |
| R |
| 2π |
| λ |
Q=[
| ||
|
| λ |
| v |
d2
| ||
| 2R |
答:
(1)导体棒运动到位置坐标为 x=
| 2n-1 |
| 4 |
(2)外力随时间t的变化关系为F=
| vd2 |
| R |
| B | 2 0 |
| 2π |
| λ |
(3)导体棒发生上个λ的位移过程中,电阻R上产生的焦耳热是
d2
| ||
| 2R |
点评:本题是产生正弦式交变电流的一种方式,运用法拉第定律、欧姆定律、安培力公式结合进行求解.中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
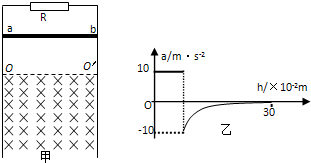 (2011?徐州一模)如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:
(2011?徐州一模)如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求: 如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:
如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求: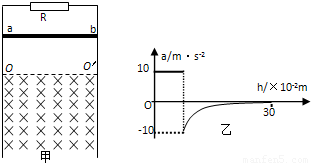 如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:
如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求: 如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:
如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求: 如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:
如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求: