题目内容
6. 如图所示,一轻绳吊着粗细均匀的棒,棒下端离地面高H,上端套着一个细环,棒和环的质量均为m,相互间最大静摩擦力等于滑动摩擦力kmg(k>1).断开轻绳,棒和环自由下落.假设棒足够长,与地面发生碰撞时,触地时间极短,无动能损失.棒在整个运动过程中始终保持竖直,空气阻力不计.求:
如图所示,一轻绳吊着粗细均匀的棒,棒下端离地面高H,上端套着一个细环,棒和环的质量均为m,相互间最大静摩擦力等于滑动摩擦力kmg(k>1).断开轻绳,棒和环自由下落.假设棒足够长,与地面发生碰撞时,触地时间极短,无动能损失.棒在整个运动过程中始终保持竖直,空气阻力不计.求:(1)从断开轻绳到棒和环都静止,摩擦力对环及棒做的总功W.
(2)从断开轻绳到棒和环都静止,棒运动的总路程x.
分析 (1)棒第一次与地面碰撞后,速度方向变为向上,环的速度方向向下,二者存在相对运动,相互间存在滑动摩擦力:棒受重力、向下的滑动摩擦力,合力方向向下;环受重力、向上的滑动摩擦力,合力方向向上.所以二者都做匀减速,当棒再次下落时,由于棒的速度小于环的下落速度,所以环的受力情况与之前相同,仍向下做匀减速运动.整个过程中能量的损失都是由于摩擦力对物体做的功,根据能量的守恒可以较简单的求得摩擦力对环及棒做的总功;
(2)棒运动的总路程为原来下降的高度H,加上第一次上升高度的两倍,对棒受力分析可以求得棒的加速度的大小,在由运动学公式可以求得上升的高度.
解答 解:(1)设环相对棒滑动距离为l
根据能量守恒 mgH+mg(H+l)=kmgl
解得$l=\frac{2H}{K-1}$
摩擦力对棒及环做的总功为:W=-kmgl
联立解得:$W=-\frac{2KmgH}{K-1}$;
(2)棒第一次弹起经过t1时间,与环达到相同速度v′1
环的速度:v′1=-v1+a环t1
棒的速度:v′1=v1+a棒t1
环的位移:${h_{环1}}=-{v_1}{t_1}+\frac{1}{2}{a_环}t_1^2$
棒的位移:${h_{棒1}}={v_1}{t_1}+\frac{1}{2}{a_棒}t_1^2$
环第一次相对棒的位移为:${x_1}={h_{环1}}-{h_{棒1}}=-\frac{2H}{k}$
棒环一起下落至地:$v_2^2-v_1^{/^2}=2g{h_{棒1}}$
解得:${v_2}=\sqrt{\frac{2gH}{k}}$
同理,环第二次相对棒的位移为${x_2}={h_{环2}}-{h_{棒2}}=-\frac{2H}{k^2}$
…${x_n}=-\frac{2H}{k^n}$
环相对棒的总位移为:x=x1+x2+…+xn
由数学规律可知:
x=$H+\frac{2k}{{{k^2}-1}}H$
答:(1)从断开轻绳到棒和环都静止,摩擦力对环及棒做的总功W为$\frac{2kmgH}{k-1}$
(2)从断开轻绳到棒和环都静止,棒运动的总路程为$H+\frac{2k}{{{k^2}-1}}H$
点评 本题考查功能关系及力与运动的关系,只要能正确受力分析,结合当速度与加速度方向相同时做加速运动,方向相反时做减速运动即可求解.


(1)根据纸带提供的信息,小华同学已经计算出了打下1、2、3、4、5这五个计数点时小车的速度,请你帮助他计算出打下计数点6时小车的速度(结果保留3位有效数字),并填入下表.
| 计数点 | 1 | 2 | 3 | 4 | 5 | 6 |
| t/s | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
| v/(m•s-1) | 0.358 | 0.400 | 0.440 | 0.485 | 0.530 | 0.570 |
(3)根据v-t图象可知,小车运动的加速度为0.43m/s2(保留2位有效数字).
(4)某同学的操作步骤如下,其中错误的步骤是AD(填代号).
A.将打点计时器固定在平板上,并接好直流电源
B.将纸带固定在小车尾部,并穿过打点计时器的限位孔
C.把一条细绳拴在小车上,细绳跨过定滑轮,下面吊着适当重的钩码
D.拉住纸带,将小车移到靠近打点计时器处先放开纸带,再接通电源
E.断开电源,取下纸带.
| A. | 研究地球绕太阳公转时的地球 | |
| B. | 研究旋转中的风力发电机转动情况时的叶片 | |
| C. | 在冰面上旋转的花样滑冰运动员 | |
| D. | 研究匀速直线运动中通过桥涵时间的火车 |
| A. | 小明上升过程中处于超重状态 | |
| B. | 研究小明在空中姿态时可把小明视为质点 | |
| C. | 起跳时地面对小明做正功使小明获得初动能 | |
| D. | 小明在下降过程中处于失重状态 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 0 |
| A. | 同种电荷相排斥,异种电荷相吸引 | B. | 库仑定律适用于所有带电体 | ||
| C. | 摩擦起电的本质是创造了电荷 | D. | 电荷量的单位是安培 |
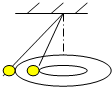
| A. | 运动的周期相同 | B. | 受到的拉力一定相同 | ||
| C. | 运动的角速度相同 | D. | 向心加速度相同 |
 将一电荷量为+Q的小球放在原来不带电的金属球附近,最终所形成的电场线分布如图所示,a、b为电场中的两点,c、d为金属球表面与内部上两点(未标出),则( )
将一电荷量为+Q的小球放在原来不带电的金属球附近,最终所形成的电场线分布如图所示,a、b为电场中的两点,c、d为金属球表面与内部上两点(未标出),则( )| A. | a点的电场强度比b点的大 | |
| B. | a点的电势比b点的高,而c、d电势不相等 | |
| C. | c点的电势比b点的高,且c、d电势相等 | |
| D. | 将检验电荷-q从a点移到b点的过程中,电场力做负功 |