题目内容
【题目】如图所示,水平放置的间距为L的足够长光滑平行金属导轨,左端接有阻值为R的定值电阻。导轨棒ab质量为m,电阻为r,与两导轨始终保持垂直并良好接触。整个装置处在磁感应强度为B的匀强磁场中,磁场方向垂直于导轨平面向里。导轨的电阻忽略不计。用水平向右的恒力F将导体棒由图示位置向右拉动。

(1)分析并说明导体棒的运动情况,并求导体棒的稳定速度vm;
(2)从微观角度看,导体棒中的自由电荷所受洛伦兹力在能量转化中起着重要作用。为了方便,可以认为导体棒中的自由电荷为正电荷。
a. 请在图中,画出自由电荷所受洛伦兹力的示意图。

b. 我们知道,洛伦兹力对运动电荷不做功。这与“动生电动势与洛伦兹力做功有关”矛盾吗?试分析当导体棒做匀速运动时,导体棒中自由电荷所受的洛伦兹力沿棒方向的分力f1和垂直于棒方向的两个分力f2哪个做正功?哪个做负功?并通过计算证明在同一过程中它们做的总功一定是零。(题目中没有出现的物理量请做必要的说明)
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)导体棒中的感应电动势E=BLv,回路中的感应电流I=E/(R+r),导体棒受到的安培力FA=BIL,由牛顿第二定律
F-![]() =ma
=ma
随着速度增大,加速度逐渐减小,当a=0时,达到稳定速度。因此导体棒先做加速度逐渐减小的加速运动,后做匀速运动。
最大速度
![]() 。
。
(2)a. 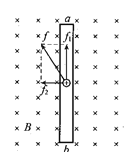
b,不矛盾;f1做正功;f2做负功;;
设导体棒向右匀速运动的速度为v1,沿导体棒定向移动的速度大小为v2,自由电荷电量为q,f1=Bqv1,f2=Bqv2;
△t时间内
沿棒方向的洛伦兹力做正功
W1=f1v2△t=Bqv1v2△t
垂直棒方向的洛伦兹力做负功
W2=-f2v1=-Bqv2v1△t
即导体棒中一个自由电荷所受的洛伦兹力做功
W1+W2=0

练习册系列答案
相关题目