题目内容
12.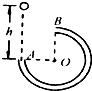 一根内壁光滑的细圆管,形状如图所示,放在竖直平面内,一个球自A口的正上方高h1处自由下落.第一次小球恰能抵达B点;第二次球自A口的正上方高h2处自由下落落入A口后,自B口射出,恰能再进入A口,则两次小球下落的高度之比h1:h2为( )
一根内壁光滑的细圆管,形状如图所示,放在竖直平面内,一个球自A口的正上方高h1处自由下落.第一次小球恰能抵达B点;第二次球自A口的正上方高h2处自由下落落入A口后,自B口射出,恰能再进入A口,则两次小球下落的高度之比h1:h2为( )| A. | 6:5 | B. | 4:5 | C. | 3:5 | D. | 2:3 |
分析 第一次释放时,恰能运动到B点,此时的速度为零,由机械能守恒就可以求得高度H;
第二次释放后,从C点飞出后做平抛运动,由平抛运动的规律可以求得在C点的初速度,在由机械能守恒可以求得此时下降的高度h.
解答 解:第一次释放时,运动到B点时的速度恰好为零,由机械能守恒得:
mgh1=mgR
所以有:h1=R
第二次释放后,从B点飞出后做平抛运动,设此时的速度大小为VB,则
水平方向为:R=VBt
竖直方向为:R=$\frac{1}{2}$gt2
解得:VB =$\sqrt{\frac{gR}{2}}$
从开始下落到B点的过程中,由机械能守恒得:
mgh2=mgR+$\frac{1}{2}$mVB2
解得:h2=$\frac{5}{4}$R
所以h1:h2=4:5
故选:B.
点评 在做题时一定要理解题目中“恰能运动到B点”,以及“恰好落回A点”这两个关键点,“恰能运动到B点”说明此时的速度为零,“恰好落回A点”说明平抛运动的水平和竖直位移都是半径R.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.关于力的作用,下列说法中正确的是( )
| A. | 用拳头击打墙壁,拳头感到疼痛,说明墙壁对拳头有作用力 | |
| B. | 用拳头击打棉花包,拳头不感到疼痛,说明棉花包对拳头没有作用力 | |
| C. | 打篮球时,接球时对手有作用力,手对球没有作用力 | |
| D. | 打篮球时,接球时球对手的作用力在先,手对球的作用力在后 |
17.在离地H高处以初速度v0竖直向下抛一个小球,若小球撞地时无机械能损失,且不计空气阻力,那么此球的回跳高度是( )
| A. | H+$\frac{v_0^2}{2g}$ | B. | H-$\frac{v_0^2}{2g}$ | C. | $\frac{v_0^2}{2g}$ | D. | $\frac{v_0^2}{g}$ |
4.做匀变速直线运动的质点,第3s内的位移是10m,则前5s内的位移( )
| A. | 一定是50m | B. | 一定不是50m | ||
| C. | 可能是50m,也可能不是50m | D. | 只有初速度为零时才是50m |
1. 如图,玻璃管内封闭了一段气体,气柱长度为l,管内外水银面高度差为h,若温度保持不变,把玻璃管稍向上提起一小段距离,则( )
如图,玻璃管内封闭了一段气体,气柱长度为l,管内外水银面高度差为h,若温度保持不变,把玻璃管稍向上提起一小段距离,则( )
 如图,玻璃管内封闭了一段气体,气柱长度为l,管内外水银面高度差为h,若温度保持不变,把玻璃管稍向上提起一小段距离,则( )
如图,玻璃管内封闭了一段气体,气柱长度为l,管内外水银面高度差为h,若温度保持不变,把玻璃管稍向上提起一小段距离,则( )| A. | h变小 | B. | h变大 | C. | l变小 | D. | l变大 |
2.关于匀速圆周运动的角速度与线速度,下列说法中不正确的是( )
| A. | 半径一定,线速度与角速度成反比 | B. | 半径一定,线速度与角速度成正比 | ||
| C. | 线速度一定,角速度与半径成反比 | D. | 角速度一定,线速度与半径成正比 |
 如图所示,用推力F推着一个重量为G=25N的木块沿着竖直墙壁向上匀速滑动,已知推力F=100N,方向与竖直方向成α=60°且斜向右上方,试求出木块与墙壁之间的动摩擦因数μ(结果保留两位有效数字).
如图所示,用推力F推着一个重量为G=25N的木块沿着竖直墙壁向上匀速滑动,已知推力F=100N,方向与竖直方向成α=60°且斜向右上方,试求出木块与墙壁之间的动摩擦因数μ(结果保留两位有效数字).