题目内容
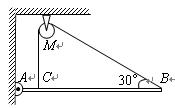
如图所示,AB为一轻质杠杆,O为支点,BO=2AO,AB两端分别悬挂实心铜球和实心铁球,杠杆在水平位置平衡,若将两球同时浸没在某液体中,液体的密度小于铜和铁的密度,则


| A.杠杆仍能保持平衡 | B.铜球一端下降 |
| C.铁球一端下降 | D.液体密度未知,故无法判断哪端下降 |
B
分析:AB两端分别悬挂实心铜球和实心铁球,杠杆在水平位置平衡,根据杠杆平衡条件求出铜块和铁块的体积关系.
当两球同时浸没在某液体中,两球受到液体的浮力作用,判断现在杠杆是否平衡.
解答:解:如图,杠杆处于平衡状态,根据杠杆平衡条件得,
OA×G铜=OB×G铁,OA×ρ铜gV铜=OB×ρ铁gV铁,
所以,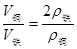 ,所以,V铜
,所以,V铜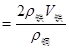 .
.
当两球同时浸没在某液体中,杠杆左端:
OA×(G铜-F浮铜)=OA×G铜-OA×F浮铜=OA×G铜-OA×ρ液gV铜=OA×G铜-OA×ρ液g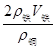 =OA×G铜-OB×ρ液g
=OA×G铜-OB×ρ液g --①
--①
杠杆右端:OB×(G铁-F浮铁)=OB×G铁-OB×F浮铁=OB×G铁-OB×ρ液gV铁--②
比较①和②式,
因为OA×G铜=OB×G铁,ρ铁<ρ铜,所以①>②,所以杠杆的左端下沉.
故选B.
点评:判断杠杆是否平衡,杠杆平衡条件是本题的关键,首先由杠杆平衡条件推知铜块和铁块的体积关系,然后根据铜块和铁块的体积关系、密度关系,判断是否符合杠杆平衡条件.力和力臂的乘积大的一端是下沉的.
当两球同时浸没在某液体中,两球受到液体的浮力作用,判断现在杠杆是否平衡.
解答:解:如图,杠杆处于平衡状态,根据杠杆平衡条件得,
OA×G铜=OB×G铁,OA×ρ铜gV铜=OB×ρ铁gV铁,
所以,
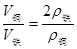 ,所以,V铜
,所以,V铜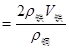 .
.当两球同时浸没在某液体中,杠杆左端:
OA×(G铜-F浮铜)=OA×G铜-OA×F浮铜=OA×G铜-OA×ρ液gV铜=OA×G铜-OA×ρ液g
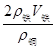 =OA×G铜-OB×ρ液g
=OA×G铜-OB×ρ液g --①
--①杠杆右端:OB×(G铁-F浮铁)=OB×G铁-OB×F浮铁=OB×G铁-OB×ρ液gV铁--②
比较①和②式,
因为OA×G铜=OB×G铁,ρ铁<ρ铜,所以①>②,所以杠杆的左端下沉.
故选B.
点评:判断杠杆是否平衡,杠杆平衡条件是本题的关键,首先由杠杆平衡条件推知铜块和铁块的体积关系,然后根据铜块和铁块的体积关系、密度关系,判断是否符合杠杆平衡条件.力和力臂的乘积大的一端是下沉的.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目