题目内容
在粗糙的水平面上,一质量为m的物体在水平恒力T作用下做加速度为a的匀加速直线运动,如在物体上再加一个恒定的推力F,并保持其加速度不变.则所加的恒力F与水平面夹角的正切值为( )
分析:根据牛顿第二定律求出物体与水平面间的动摩擦因数.根据力的独立作用原理,当所加的恒力所引起的物体动力的变化量与阻力变化量相等时同,物体的加速度不变,由平行四边形定则求出恒力F与水平面夹角的正切值.
解答:解:未加恒力F时,根据牛顿第二定律得: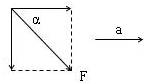
T-μmg=ma
得到,μ=
设恒力F与水平面夹角为α,如图,当所加的恒力所引起的物体动力的变化量与阻力变化量相等时同,物体的加速度不变,则有
Fcosα=μFsinα
得tanα=
=
故选B

T-μmg=ma
得到,μ=
| T-ma |
| mg |
设恒力F与水平面夹角为α,如图,当所加的恒力所引起的物体动力的变化量与阻力变化量相等时同,物体的加速度不变,则有
Fcosα=μFsinα
得tanα=
| 1 |
| μ |
| mg |
| T-ma |
故选B
点评:本题运用力的独立作用原理,只研究恒力F引起的效果,也可以对物体受到的所有的力进行分析,根据牛顿第二定律求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
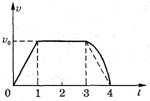 在粗糙的水平面上,一物块在水平方向的外力F的作用下做直线运动,其v-t图象如图中实线所示,则下列判断中正确的是( )
在粗糙的水平面上,一物块在水平方向的外力F的作用下做直线运动,其v-t图象如图中实线所示,则下列判断中正确的是( )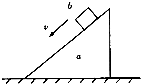 如图所示,在粗糙的水平面上放一斜面体a,若物块b在a的斜面上匀速下滑,则下列说法正确的是( )
如图所示,在粗糙的水平面上放一斜面体a,若物块b在a的斜面上匀速下滑,则下列说法正确的是( ) (2013?虹口区二模)在粗糙的水平面上,一物块在水平方向的外力F的作用下做初速为v0的运动,其速度时间v-t图象如图所示,则下列判断中正确的是( )
(2013?虹口区二模)在粗糙的水平面上,一物块在水平方向的外力F的作用下做初速为v0的运动,其速度时间v-t图象如图所示,则下列判断中正确的是( )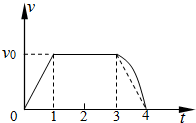 在粗糙的水平面上,一物块在水平方向的外力F的作用下做直线运动,其v-t图象如图中实线所示,则下列判断中错误的是( )
在粗糙的水平面上,一物块在水平方向的外力F的作用下做直线运动,其v-t图象如图中实线所示,则下列判断中错误的是( )