题目内容
5.如图甲所示,MN、PQ为间距L=0.5m足够长的平行导轨,NQ⊥MN,导轨的电阻均不计.导轨平面与水平面间的夹角θ=37°,NQ间连接有一个R=4Ω的电阻.有一匀强磁场垂直于导轨平面且方向向上,磁感应强度为B0=1T.将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好.现由静止释放金属棒,当金属棒滑行至cd处时达到稳定速度,已知在此过程中通过金属棒截面的电量q=0.2C,且金属棒的加速度a与速度v的关系如图乙所示,设金属棒沿导轨向下运动过程中始终与NQ平行.(取g=10m/s2,sin37°=0.6,cos37°=0.8).求:(1)金属棒与导轨间的动摩擦因数μ;
(2)cd离NQ的距离s;
(3)金属棒滑行至cd处的过程中,电阻R上产生的热量;
(4)若将金属棒滑行至cd处的时刻记作t=0,从此时刻起,让磁感应强度逐渐减小,为使金属棒中不产生感应电流,则磁感应强度B应怎样随时间t变化(写出B与t的关系式).
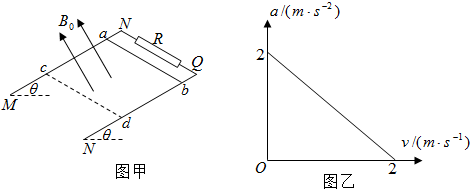
分析 (1)当刚释放时,导体棒中没有感应电流,所以只受重力、支持力与静摩擦力,由牛顿第二定律可求出动摩擦因数.
(2)当金属棒速度稳定时,则受到重力、支持力、安培力与滑动摩擦力达到平衡,这样可以列出安培力公式,产生感应电动势的公式,再由闭合电路殴姆定律,列出平衡方程可求出金属棒的内阻,从而利用通过棒的电量来确定发生的距离.
(3)金属棒滑行至cd处的过程中,由动能定理可求出安培力做的功,而由于安培力做功导致电能转化为热能.
(4)要使金属棒中不产生感应电流,则穿过线框的磁通量不变.同时棒受到重力、支持力与滑动摩擦力做匀加速直线运动.从而可求出磁感应强度B应怎样随时间t变化的.
解答 解:(1)当v=0时,a=2m/s2
由牛顿第二定律得:mgsinθ-μmgcosθ=ma
代入数据解得:μ=0.5
(2)由图象可知:vm=2m/s
当金属棒达到稳定速度时,有:FA=B0IL;
且:B0IL+μmgcosθ=mgsinθ
代入数据解得:I=0.2A;
切割产生的感应电动势为:E=B0Lv=1×0.5×2=1V;
因$I=\frac{E}{R+r}$,
代入数据解得:r=1Ω
电量为:$q=It=n\frac{△φ}{△t(R+r)}t=n\frac{△φ}{R+r}$
而△φ=△B×L×s
即有:s=2m
(3)$mgh-μmgscos{37^0}-{W_F}=\frac{1}{2}m{v^2}-0$
产生热量:WF=Q总=0.1J
${Q_R}=\frac{4}{5}{Q_总}=0.08J$
(4)当回路中的总磁通量不变时,
金属棒中不产生感应电流.
此时金属棒将沿导轨做匀加速运动.
牛顿第二定律:mgsinθ-μmgcosθ=ma
a=g(sinθ-μcosθ)=10×(0.6-0.5×0.8)m/s2=2m/s2
${B_0}Ls=BL({s+vt+\frac{1}{2}a{t^2}})$
则磁感应强度与时间变化关系:$B=\frac{{{B_0}s}}{{s+υt+\frac{1}{2}a{t^2}}}=\frac{2}{{2+2t+{t^2}}}$.
答:(1)金属棒与导轨间的动摩擦因数为0.5;
(2)cd离NQ的距离2m;
(3)金属棒滑行至cd处的过程中,电阻R上产生的热量0.08J;
(4)若将金属棒滑行至cd处的时刻记作t=0,从此时刻起,让磁感应强度逐渐减小,为使金属棒中不产生感应电流,则磁感应强度B应怎样随时间t变化为$B=\frac{2}{2+2t+{t}^{2}}$.
点评 本题考查了牛顿运动定律、闭合电路殴姆定律,安培力公式、感应电动势公式,还有动能定理.同时当金属棒速度达到稳定时,则一定是处于平衡状态,原因是安培力受到速度约束的.还巧妙用磁通量的变化去求出面积从而算出棒的距离.最后线框的总磁通量不变时,金属棒中不产生感应电流是解题的突破点.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案| A. | 汽车每秒钟内速度变化 0.5 m/s | |
| B. | 汽车每秒钟内加速度变化 0.5 m/s2 | |
| C. | 汽车的初速度比前 1 秒内的末速度大 0.5 m/s | |
| D. | 汽车在任意 1 s 内的末速度等于初速度的 0.5 倍 |
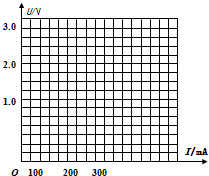 某实验小组预测定一只小灯泡(其额定功率为0.75w,但额定电压已经模糊不清)的额定电压值,实验过程如下:
某实验小组预测定一只小灯泡(其额定功率为0.75w,但额定电压已经模糊不清)的额定电压值,实验过程如下:他们先用多用电表的欧姆档测出小灯泡的电阻约为2Ω,然后根据公式算出小灯泡的额定电压U=$\sqrt{pR}$≈1.23v.但他们认为这样求得的额定电压值不准确,于是他们利用实验室中的器材设计了一个实验电路,进行进一步的测量.他们选择的实验器材有:
A.电压表V(量程3v,内阻约3kΩ)
B.电流表A1(量程150mA,内阻约2Ω)
C.电流表A2(量程500mA,内阻约0.6Ω)
D.滑动变阻器R1(0~20Ω)
E.滑动变阻器R2(0~50Ω)
F.电源E(电动势4.0v,内阻不计)
G.开关s和导线若干
(1)测量过程中他们发现,当电压达到1.23v时,灯泡亮度很弱,继续缓慢地增加电压,当达到2.70v时,发现灯泡已过亮,立即断开开关,所有测量数据见表:
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| U/V | 0.20 | 0.60 | 1.00 | 1.40 | 1.80 | 2.20 | 2.70 |
| I/mA | 80 | 155 | 195 | 227 | 255 | 279 | 310 |
(2)从表中的实验数据可以知道,他们在实验时所选择的电路应为C,电流表应选A2(填“A1”或“A2”),滑动变阻器应选R1(填“R1”或“R2”).
| A. | 月球表面的重力加速度g月=$\frac{2h{{v}_{0}}^{2}}{{L}^{2}}$ | |
| B. | 月球的质量g月=$\frac{2h{R}^{2}{{v}_{0}}^{2}}{G{L}^{2}}$ | |
| C. | 月球的第一宇宙速度v=$\frac{{v}_{0}}{L}$$\sqrt{2hR}$ | |
| D. | 月球的平均密度ρ=$\frac{3h{{v}_{0}}^{2}}{2πG{L}^{2}}$ |
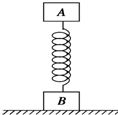 如图所示,质量相等的两木块中间连有一弹簧,今用力F缓慢向上提A,直到B恰好离开地面.开始时物体A静止在弹簧上面.设开始时弹簧的弹性势能为Ep1,B刚要离开地面时,弹簧的弹性势能为Ep2,则关于Ep1、Ep2大小关系及弹性势能变化△Ep说法中正确的是( )
如图所示,质量相等的两木块中间连有一弹簧,今用力F缓慢向上提A,直到B恰好离开地面.开始时物体A静止在弹簧上面.设开始时弹簧的弹性势能为Ep1,B刚要离开地面时,弹簧的弹性势能为Ep2,则关于Ep1、Ep2大小关系及弹性势能变化△Ep说法中正确的是( )| A. | Ep1=Ep2 | B. | Ep1>Ep2 | C. | △Ep>0 | D. | △Ep<0 |

| A. | 在0~t1时间内,导线框中电流的方向为abcda | |
| B. | 在0~t1时间内,导线框中电流越来越小 | |
| C. | 在t1~t2时间内,导线框中电流保持不变 | |
| D. | 在t1~t2时间内,导线框bc边受到安培力大小保持不变 |
| A. | 物体没做功,则物体就没有能量 | |
| B. | 动摩擦力只能做负功 | |
| C. | 重力对物体做功,物体的重力势能可能增加 | |
| D. | 重力对物体做功,物体的重力势能一定减少 |
 一理想变压器原、副线圈匝数比n1:n2=2:1,原线圈与正弦交变电源连接,输入电压u随时间t变化的规律如图所示,副线圈接一个R=10Ω 的电阻,则( )
一理想变压器原、副线圈匝数比n1:n2=2:1,原线圈与正弦交变电源连接,输入电压u随时间t变化的规律如图所示,副线圈接一个R=10Ω 的电阻,则( )| A. | 电阻R两端电压的有效值为50V | |
| B. | 电阻R中电流的频率为0.25Hz | |
| C. | 1分钟内电阻R产生的热量为1.5×103J | |
| D. | 变压器的输入功率为250W |
 在“研究匀变速直线运动”的实验中,得到的一条纸带如图所示,纸带上每相邻的两计数点间的时间间隔均为0.1s,测得A到B和B到C的距离分别为5.60cm和8.62cm,则物体的加速度大小为3.02m/s2,B点对应的速度大小为0.711 m/s.
在“研究匀变速直线运动”的实验中,得到的一条纸带如图所示,纸带上每相邻的两计数点间的时间间隔均为0.1s,测得A到B和B到C的距离分别为5.60cm和8.62cm,则物体的加速度大小为3.02m/s2,B点对应的速度大小为0.711 m/s.