题目内容
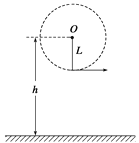
【题目】如果把水星和金星绕太阳的运动视为匀速圆周运动，从水星与金星在一条直线上开始计时，如图所示。若天文学家测得在相同时间
内水星转过的角度为θ1；金星转过的角度为θ2(θ1、θ2均为锐角)，且已知水星离太阳表面的高度和太阳的半径之比为k，则由此条件可求得
A. 水星和金星绕太阳运动的周期之比
B. 水星和金星的密度之比
C. 水星和金星的动能之比
D. 太阳的密度
【答案】AD
【解析】试题分析：根据相同时间内转过的角度之比求出角速度之比，从而得出周期之比，根据万有引力提供向心力得出轨道半径和周期的关系，结合水星离太阳表面的高度和太阳的半径之比为k．求解出太阳半径表达式，根据密度公式计算太阳的密度，
相同时间内水星转过的角度为
；金星转过的角度为
，可知它们的角速度之比为
： 
．周期
，则周期比为
： 
，故A正确；水星和金星是环绕天体，无法求出质量，所以求不出密度比，以及动能之比，故BC错误；根据
可得水星的运动半径为
，设太阳的半径为R，水星到太阳表面的高度为h，则
， 
，联立解得
，故太阳的密度为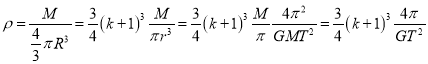
，故D正确．
练习册系列答案
相关题目
