��Ŀ����
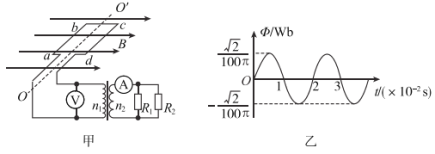
����Ŀ����ͼ��ʾ������ΪM���㹻����������PQMN���ڹ⻬�ľ�Եˮƽ���ϣ�һ����ΪR������Ϊm�ĵ����ef�����ڵ����ϣ����뵼���⻬��ʼ���뵼��Ӵ����ã����Ҳ��������̶���ˮƽ��Ĺ⻬����c��d����PQcd���������Ρ�����PQ�ε���Ϊr����ΪL����ʼʱ����cdΪ�߽磨ͼ��������ʾ�������Ҳർ�����Ϊ�㣬��ǿ�ų�������ֱ���£�����ർ�쵥λ���ȵĵ���ΪR����ǿ�ų�ˮƽ���ң��Ÿ�Ӧǿ�ȴ�С��ΪB����t��0ʱ��һˮƽ���ҵ�����F��ֱ�����ڵ����PQ���ϣ�ʹ�����ɾ�ֹ��ʼ�����ٶ�Ϊa���ȼ���ֱ���˶����������ٶ�ȡg����
(1)��t1ʱ�䣬��·�д�ͨ���ı仯����
(2)ˮƽ���ҵ�����F��ʱ��仯�Ĺ�ϵʽ��
(3)��F=0����������PQMN��ֹ��cd�Ҳ�ų���������![]() �ﵽ��ֵʱ�������ef�պöԹ����ѹ����
�ﵽ��ֵʱ�������ef�պöԹ����ѹ����

���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() ��
��
��������
(1)��![]() ʱ�䣬��·�����Ϊ
ʱ�䣬��·�����Ϊ
![]()
��·�д�ͨ��
![]()
��·�д�ͨ���ı仯��
![]()
(2) ���ݷ����ڵ�Ÿ�Ӧ���ɣ�ijʱ��PQ�����ĸ�Ӧ�綯��ΪE
![]()
���������ٶ�Ϊ����ȼ����˶�
![]()
����
![]()
�ɱպϵ�·ŷķ���ɵø�Ӧ����
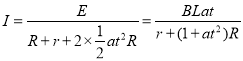
PQ�����ܵİ�������С
![]()
�Ե��죬��ţ�ٵڶ�������
![]()
�������
![]()
(3)��![]() ����������PQMN��ֹ��cd�Ҳ�ų���������ef�պöԹ����ѹ����
����������PQMN��ֹ��cd�Ҳ�ų���������ef�պöԹ����ѹ����
��ƽ��������
![]()
�ɷ����ڵ�Ÿ�Ӧ������
![]()
![]()
������������
![]()

 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�