题目内容
16.一汽车重4t,途经一圆弧形拱桥,圆弧半径为20m.若桥最高处能承受的最大压力为2.94×104N,则汽车速度多大时才能安全开过桥顶?(g取9.8m/s2)分析 以汽车为研究对象,分析受力可知,过桥顶时由重力和桥顶的支持力的合力提供汽车的向心力,当桥对汽车的支持力最小时,求出最小速度.当桥对汽车的支持力为零时,根据牛顿运动定律求出最大速度,从而得到汽车过桥顶时速度范围.
解答 解:汽车以速度v开过圆弧形拱桥顶,有:mg-FN=m$\frac{{v}^{2}}{R}$.
当桥最高处承受的最大压力为FN′=2.94×104N时,FN=FN′=2.94×104N,代入上式,可求得汽车安全过桥的最小速度为:v1=$\sqrt{\frac{(mg-{F}_{N})R}{m}}$=7 m/s
当FN=0(桥面不受力)时,有:mg=m$\frac{{v}_{2}^{2}}{R}$
求得汽车安全过桥的最大速度为:v2=$\sqrt{gR}$=$\sqrt{10×20}$m/s=10$\sqrt{2}$ m/s
(当v>14m/s时,汽车将飞过桥顶,那是不安全的).故当7m/s≤v<10$\sqrt{2}$ m/s时,汽车可安全开过桥顶.
答:汽车速度在7m/s≤v<10$\sqrt{2}$ m/s时才能安全开过桥顶.
点评 本题是生活实际中圆周运动问题,要学会分析受力,确定圆周运动的临界条件,运用牛顿运动定律研究.

练习册系列答案
相关题目
7.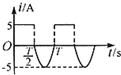 如图所示的交变电流,其中每个周期的后半周期的图象为半个周期的正弦曲线,该交流电流的有效值是( )
如图所示的交变电流,其中每个周期的后半周期的图象为半个周期的正弦曲线,该交流电流的有效值是( )
 如图所示的交变电流,其中每个周期的后半周期的图象为半个周期的正弦曲线,该交流电流的有效值是( )
如图所示的交变电流,其中每个周期的后半周期的图象为半个周期的正弦曲线,该交流电流的有效值是( )| A. | 2.5$\sqrt{3}$A | B. | 5A | C. | 2.5$\sqrt{2}$A | D. | 2.5A |
4.发电厂发电机的输出电压为U1,发电厂至用户的输电导线的总电阻为R,通过输电导线的电流为I,输电线末端的电压为U2,下面选项表示输电导线上损耗的功率不正确的是( )
| A. | $\frac{{U}_{1}^{2}}{R}$ | B. | $\frac{({U}_{1}-{U}_{2})^{2}}{R}$ | C. | I2R | D. | I(U1一U2) |
11.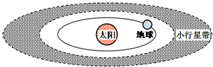 如图所示,在地球轨道外侧有一小行星带.假设行星带中的小行星都只受到太阳的引力,并绕太阳做匀速圆周运动.下列说法正确的是( )
如图所示,在地球轨道外侧有一小行星带.假设行星带中的小行星都只受到太阳的引力,并绕太阳做匀速圆周运动.下列说法正确的是( )
 如图所示,在地球轨道外侧有一小行星带.假设行星带中的小行星都只受到太阳的引力,并绕太阳做匀速圆周运动.下列说法正确的是( )
如图所示,在地球轨道外侧有一小行星带.假设行星带中的小行星都只受到太阳的引力,并绕太阳做匀速圆周运动.下列说法正确的是( )| A. | 各小行星绕太阳运动的周期小于一年 | |
| B. | 小行星带内各行星绕太阳公转的线速度均小于地球公转的线速度 | |
| C. | 小行星带内侧行星的加速度小于外侧行星的加速度 | |
| D. | 与太阳距离相等的每一颗小行星,受到太阳的引力大小都相等 |
1.一定质量理想气体处于平衡状态Ⅰ,现使其温度降低而压强升高,达到平衡状态Ⅱ,则以下判断正确的是( )
| A. | 状态Ⅰ时气体的密度比状态Ⅱ时的大 | |
| B. | 状态Ⅰ时各个分子的动能比状态Ⅱ时的大 | |
| C. | 状态Ⅰ时分子的平均距离比状态Ⅱ时的大 | |
| D. | 状态Ⅰ时单个分子对器壁平均撞击力比状态Ⅱ时小 |
8.下列说法中正确的有( )
| A. | 实验“用油膜法估测分子大小”中,油酸分子的直径等于油酸酒精溶液的体积除以相应油酸膜的面积 | |
| B. | 布朗运动中,悬浮在液体中的固体颗粒越小、液体的温度越高,布郎运动越激烈 | |
| C. | 分子间的距离越小,分子间引力越小,斥力越大 | |
| D. | 液晶的光学性质与某些晶体相似,具有各向异性 |
5.下列说法中正确的是( )
| A. | 物体只要存在加速度,物体的速度就增大 | |
| B. | 只要物体的加速度为正,物体的速度一定增大 | |
| C. | 物体的加速度增大,物体的速度一定增大 | |
| D. | 加速度在减小,物体的速度可能增大 |
6.小船在静水中的速度为3m/s.它在一条流速为4m/s、河宽为150m的河流中渡河,则( )
| A. | 小船不可能垂直河岸到达河对岸 | |
| B. | 小船渡河的时间可能为40s | |
| C. | 小船渡河的时间至少为30s | |
| D. | 小船若在50s内渡河,到达河对岸时被冲下150m远 |