Question

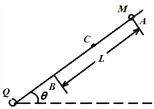
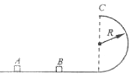
【题目】如图所示，静止在光滑水平面上的小滑块A和B，质量分别为2m和m；现给小滑块A水平向右的瞬间冲量，小滑块向右运动与小骨块B发生正碰，并粘在一起，恰好能通过半径为R的半圆形光滑轨道最高点C，飞出后做平抛运动，重力加速度为g。求：

(1)小滑块在最高点C的速度大小；

(2)小滑块落地点到C点的水平距离；

(3)小滑块A开始受到的瞬间冲量大小I。

Answer 1

【答案】(1),(2) 2R,(3).

【解析】(1) 小滑块恰好通过轨道最高点，NC=0：

由牛顿第二定律得： (2m＋m)g =(2m＋m)

vC＝

(2) 小滑块从C点飞出做平抛运动

竖直方向：2R＝gt2

t＝2

水平方向：x = vCt＝2R

(3)滑块A、B正碰后粘在一起的速度是v，从圆形轨道最低点到最高点过程中，由动能定理得：－(2m＋m)g·2R＝(2m＋m) (vC2－v2)

解得：v＝

滑块A、B正碰，由动量守恒得：2m vA= (2m＋m) v

对滑块A，由动量定理可知：

滑块A受到的冲量I＝△p=2m vA= (2m＋m) v=3m