题目内容
14.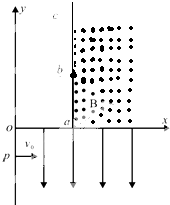 如图所示的平面直角坐标系xoy,在第Ⅳ象限内有平行于y轴的匀强电场,方向沿y轴负方向;在第Ⅰ象限的ac右侧区域内有匀强磁场,ac垂直于x轴,方向垂直于xoy平面向外,ab长为L,且ac边与y轴平行.一质量为m、电荷量为q的负粒子,从y轴上的P(0,-h)点,以大小为v0的速度沿x轴正方向射入电场,通过电场后从x轴上的a(2h,0)点进入第Ⅰ象限,又经过磁场从b点离开磁场,不计粒子所受的重力.求:
如图所示的平面直角坐标系xoy,在第Ⅳ象限内有平行于y轴的匀强电场,方向沿y轴负方向;在第Ⅰ象限的ac右侧区域内有匀强磁场,ac垂直于x轴,方向垂直于xoy平面向外,ab长为L,且ac边与y轴平行.一质量为m、电荷量为q的负粒子,从y轴上的P(0,-h)点,以大小为v0的速度沿x轴正方向射入电场,通过电场后从x轴上的a(2h,0)点进入第Ⅰ象限,又经过磁场从b点离开磁场,不计粒子所受的重力.求:(1)电场强度E的大小;
(2)粒子到达a点时速度的大小和方向;
(3)ac右侧区域内磁场的磁感应强度B的大小.
分析 (1)粒子在电场中做类平抛运动,水平位移和竖直位移均已知,由牛顿第二定律和运动学公式,运用运动的分解法可求出场强大小E;
(2)由速度的合成法求出粒子到达a点时速度大小和方向;
(3)粒子在磁场中做匀速圆周运动,作出轨迹,由几何知识求出半径,由牛顿第二定律列式即可求出磁感应强度大小.
解答 解:(1)粒子在第电场内做类平抛运动,设类平抛运动的时间为t1,则
水平方向有:2h=v0t1
竖直方向有:h=$\frac{1}{2}\frac{qE}{m}{t}_{1}^{2}$
联立解得:E=$\frac{m{v}_{0}^{2}}{2qh}$
(2)设粒子到达a点时时竖直方向的速度vy
则有:vy=at1=$\frac{qE}{m}$t1
联立解得:vy=v0
所以粒子到达a点时速度大小为v=$\sqrt{2}$v0
与x轴的夹角为θ,由几何关系得:tanθ=$\frac{{v}_{y}}{{v}_{0}}$=1,
所以θ=45°;
(3)进入磁场后做匀速圆周运动,轨迹如图所示:
结合几何关系,有:r=Lsin45°=$\frac{\sqrt{2}}{2}L$
洛仑兹力提供向心力,故:
$qvB=m\frac{v^2}{r}$
联立解得:B=$\frac{2m{v}_{0}}{qL}$
答:(1)电场强度E的大小为$\frac{m{v}_{0}^{2}}{2qh}$;
(2)粒子到达a点时速度的大小为$\sqrt{2}{v}_{0}$,与+x轴成45°斜向右上;
(3)ac右侧区域内磁场的磁感应强度B的大小为$\frac{2m{v}_{0}}{qL}$.
点评 该题考查了有边界电磁场的问题,在电场中的偏转,利用平抛运动的知识求解;粒子在有边界的匀强磁场中运动,利用几何关系求解运动半径和转过的圆心角是解决问题的关键.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案| A. | 在超重现象中,物体的重力是增大的 | |
| B. | 游泳运动员仰卧在水面静止不动时处于失重状态 | |
| C. | 如果物体处于失重状态,它必然有向下的加速度 | |
| D. | 处于完全失重状态的物体,其重力为零 |
| A. | 仅凭上述信息及T、g′能算出月球的半径 | |
| B. | 仅凭上述信息及T、g′能算出月球上的第一宇宙速度 | |
| C. | 仅凭上述信息及T、g′能算出月球的质量和密度 | |
| D. | 卫星沿绕地球椭圆轨道运行时,卫星上的仪器处于失重状态 |

| A. | ωA=ωB | B. | ωA:ωB=1:2 | C. | ωA:ωB=2:1 | D. | 无法计算 |
 如图所示,在光滑绝缘水平面上,两个带等量负电的点电荷分别固定在A、B两点,O为AB连线的中点,MN为AB的垂直平分线.在MN之间的C点由静止释放一个带正电的小球(可视为质点),若不计空气阻力,则( )
如图所示,在光滑绝缘水平面上,两个带等量负电的点电荷分别固定在A、B两点,O为AB连线的中点,MN为AB的垂直平分线.在MN之间的C点由静止释放一个带正电的小球(可视为质点),若不计空气阻力,则( )| A. | C点的场强大于O点的场强,C点的电势高于O点的电势 | |
| B. | 小球从C点运动至距离该点最远位置的过程中,其所经过各点所受的电场力先减小后增大 | |
| C. | 小球从C点运动至距离该点最远位置的过程中,其电势能先减小后增大 | |
| D. | 若在小球运动过程中,两个点电荷所带电荷量同时等量地缓慢增大,则小球往复运动过程中的最大速度将逐渐减小 |
 质量为m的带正电粒子,电荷量为q,不计重力,以速度v0从y轴上的a点射入图中第一象限,v0与y轴成30°角,为了使该带电粒子能从x轴上的b点以与x轴上的b点以与x轴成60°角的速度射出,可在适当的地方加一个垂直于xOy平面、磁感强度为B的匀强磁场,若此磁场分布在一个圆形区域内,试求这个圆形磁场区域的最小面积.
质量为m的带正电粒子,电荷量为q,不计重力,以速度v0从y轴上的a点射入图中第一象限,v0与y轴成30°角,为了使该带电粒子能从x轴上的b点以与x轴上的b点以与x轴成60°角的速度射出,可在适当的地方加一个垂直于xOy平面、磁感强度为B的匀强磁场,若此磁场分布在一个圆形区域内,试求这个圆形磁场区域的最小面积.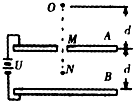 如图所示,A、B为平行板电容器,两板相距d,接在电压为U的电源上,在A板的中央有一小孔M(两板间电场可视为匀强电场).今有一质量为m的带电质点,自A板上方与A板相距也为d的O点由静止自由下落,穿过小孔M后到达距B板$\frac{d}{2}$的N点时速度恰好为零.求:
如图所示,A、B为平行板电容器,两板相距d,接在电压为U的电源上,在A板的中央有一小孔M(两板间电场可视为匀强电场).今有一质量为m的带电质点,自A板上方与A板相距也为d的O点由静止自由下落,穿过小孔M后到达距B板$\frac{d}{2}$的N点时速度恰好为零.求: