题目内容
7．
两根光滑绝缘棒在同一竖直平面内，两棒与水平面间均成45°角，棒上各穿有一个质量为m、带电荷量为Q的相同小球，如图所示，现让两小球相距多远时，小球的速度达到最大值？
分析 根据加速度为零时，速度达到最大，结合库仑定律，即可求解．
解答 
解：经分析，当速度达到最大时，其在棒方向的加速度为零，
即Gcos45°-F库cos45°=0；
又库仑定律可知，F库=$\frac{k{Q}^{2}}{{r}^{2}}$=mg；
代入数据，解得：r=$\sqrt{\frac{k{Q}^{2}}{mg}}$．
答：两球从上述位置同时下滑，当它们相距$\sqrt{\frac{k{Q}^{2}}{mg}}$时，两球速度最大．
点评 考查库仑定律与牛顿第二定律的应用，注意加速度为零时，速度达到最大，同时注意正确的运算．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
15．日常生活中，对平均速度和瞬时速度我们都称“速度”．下列所说的速度中，哪些是平均速度？（ ）
| A． | 网球比赛中发球是至关重要的一环，罗迪克曾在戴维斯杯半决赛中发球时速达到249km/h千米，近几年尚无人超越 | |
| B． | 经提速后列车的速度达到150km/h | |
| C． | 由于堵车，在隧道内的车速仅为1.2m/s | |
| D． | 返回地面的“神舟七号”飞船以4m/s的速度落地 | |
| E． | 子弹以800m/s的速度撞击在墙上 |
一负电荷从电场中A点由静止释放，只受静电力作用，沿电场线运动到B点，它运动的v-t图象如图所示，则两点A、B所在区域的电场线分布情况可能是下图中的（ ）
12．上海锦江乐园新建的“摩天转轮”，它的直径达98m，世界排名第五．游人乘坐时，转轮始终不停地匀速转动，每转一周用时25min，下列说法中正确的是（ ）
| A． | 每时每刻，每个乘客受到的合力都不等于零 | |
| B． | 每个乘客都在做加速度为零的匀速运动 | |
| C． | 乘客在乘坐过程中对座位的压力始终不变 | |
| D． | 乘客运动的加速度始终保持不变 |
19．
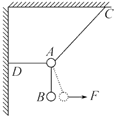如图所示，三根轻细绳悬挂两个质量相同的小球保持静止，A、D间细绳是水平的，现对B球施加一个水平向右的力F，将B缓缓拉到图中虚线位置，这时三根细绳张力${\;}_{{T}_{AC}}$、${\;}_{{T}_{AD}}$、${\;}_{{T}_{AB}}$的变化情况是（ ）
如图所示，三根轻细绳悬挂两个质量相同的小球保持静止，A、D间细绳是水平的，现对B球施加一个水平向右的力F，将B缓缓拉到图中虚线位置，这时三根细绳张力${\;}_{{T}_{AC}}$、${\;}_{{T}_{AD}}$、${\;}_{{T}_{AB}}$的变化情况是（ ）| A． | 都变大 | B． | ${\;}_{{T}_{AD}}$和${\;}_{{T}_{AB}}$变大，${\;}_{{T}_{AC}}$不变 | ||
| C． | ${\;}_{{T}_{AC}}$和${\;}_{{T}_{AB}}$变大，${\;}_{{T}_{AD}}$不变 | D． | ${\;}_{{T}_{AC}}$和${\;}_{{T}_{AD}}$变大，${\;}_{{T}_{AB}}$不变 |