题目内容
(13分)如图所示，匀强磁场的磁感应强度B=2 T，匝数n=6的矩形线圈abcd绕中心轴OO′匀速转动，角速度ω=200 rad/s。已知ab=0.1 m，bc=0.2 m，线圈的总电阻R=40Ω，试求：
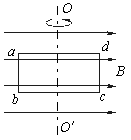(1)线圈中感应电动势的最大值和感应电流的最大值；
(2)设时间t=0时线圈平面与磁感线垂直，写出线圈中感应电动势的瞬时值表达式；
(3)当ωt=30°时，穿过线圈的磁通量和线圈中的电流的瞬时值；
(4)线圈从图示位置转过
的过程中，感应电动势的平均值。
解析：
（1）因为线圈匀速转动，感应电动势的最大值就出现在图示位置
Em=nBSω
=6×2×0.1×0.2×200 V=48 V………①（2分）
感应电流最大值
Im=
A=1.2 A………………②（1分）
（2）感应电动势的瞬时值表达式：
e=Em?sinωt=48sin200t V……………③（2分）
（3）当ωt=30°角时，穿过线圈的磁通量为Φ，则
Φ=Bs?cos30°
=2×0.1×0.2×
Wb=0.035Wb……④（2分）
此时感应电动势瞬时值为：
e=48sin30°V=48×
V=24 V…………⑤（1分）
由欧姆定律可得此时电流瞬时值为：
i=
A
=0.6 A……⑥（1分）
（4）线圈从图示位置转过
的过程中，磁通量的变化为
ΔΦ=B?S……………………………⑦（1分）
线圈转过所用的时间Δt=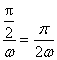
……⑧（1分）
此过程中交变电动势的平均值
=n?
≈30.6 V…………⑨（2分）
练习册系列答案
相关题目
神舟十号在酒泉卫星发射中心“921工位”，2013年6月11日17时38分，由长征二号F改进型运载火箭（遥十）“神箭”成功发射．在轨飞行十五天左右，加上发射与返回，其中停留天宫一号十二天，6月13日与天宫一号进行对接．．假如神舟十号与天宫一号对接前所处的轨道如图所示，当它们处于如图所示的轨道运行时，下列说法正确的是（ ）
