题目内容
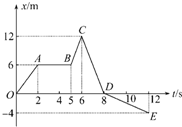
6. 某空降兵进行军事演习,为以最快的速度到达地面,士兵以v0的初速度从悬停的直升飞机上跳下,在t1时刻,速度达到v1时打开降落伞,做减速运动,为保证士兵安全,在t2时刻以较小速度v2着地,其v-t图象如图所示,则 ( )
某空降兵进行军事演习,为以最快的速度到达地面,士兵以v0的初速度从悬停的直升飞机上跳下,在t1时刻,速度达到v1时打开降落伞,做减速运动,为保证士兵安全,在t2时刻以较小速度v2着地,其v-t图象如图所示,则 ( )| A. | 在t1~t2时间内,士兵的加速度大小逐渐增大 | |
| B. | 在0~t1时间内,士兵的位移大小s>$\frac{{v}_{1}+{v}_{2}}{2}$t1 | |
| C. | 在t1~t2时间内,士兵的平均速度$\overline{v}$=$\frac{{v}_{1}+{v}_{2}}{2}$ | |
| D. | 在t1~t2时间内,士兵的位移大小s<$\frac{{v}_{1}+{v}_{2}}{2}$(t2-t1) |
分析 速度图象倾斜的直线表示物体做匀加速直线运动,其加速度不变.根据斜率等于加速度,分析t1~t2时间内加速度如何变化.根据牛顿第二定律分析阻力如何变化.根据“面积”等于位移,将在t1~t2的时间内物体的位移与匀减速直线运动的位移进行比较,再分析平均速度与的大小$\frac{{v}_{1}+{v}_{2}}{2}$的大小.
解答 解:A、t1~t2时间内图线的斜率逐渐减小,则加速度逐渐减小.故A错误;
B、在0~t1时间内士兵做匀加速直线运动,平均速度$\overline{{v}_{1}}$=$\frac{{v}_{1}+{v}_{2}}{2}$,则士兵的位移大小s=$\frac{{v}_{1}+{v}_{2}}{2}$t1.故B错误;
C、在t1~t2时间内,假设伞兵做匀减速直线运动,其平均速度为$\frac{{v}_{1}+{v}_{2}}{2}$.根据“面积”等于位移可知,匀减速直线运动的位移大于伞兵实际运动的位移,则平均速度v<$\frac{{v}_{1}+{v}_{2}}{2}$,所以t1~t2时间内,士兵的位移大小s<$\frac{{v}_{1}+{v}_{2}}{2}$(t2-t1).故C错误,D正确.
故选:D
点评 本题根据斜率等于加速度判断加速度的变化.根据“面积”等于位移,分析平均速度的大小.对于匀变速直线运动的平均速度才等与$\frac{{v}_{1}+{v}_{2}}{2}$.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
16.下列说法正确的是( )
| A. | 根据I=$\frac{U}{R}$可知,流过导体的电流与加在它两端的电压成正比,与其电阻的大小成反比 | |
| B. | 根据R=$\frac{U}{l}$可知,导体电阻的大小与加在它两端的电压成正比,与通过它的电流成反比 | |
| C. | 欧姆定律适用于金属导体、电解质溶液导电、电离后气体导电和晶体二极管导电 | |
| D. | 欧姆定律只适用于纯电阻电路 |
11.关于磁感线和电场线,下述说法正确的是( )
| A. | 磁体周围的磁感线都是从磁体的北极出发,到南极终止 | |
| B. | 磁感线和电场线都是一些互相平行的曲线 | |
| C. | 磁感线是闭合曲线,而静电场的电场线不是闭合曲线 | |
| D. | 磁感线和电场线都只能分别表示磁场和电场的方向 |
18.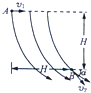 空间某区域存在着电场,电场线在竖直面上的分布如图所示,一个质量为m、电量为q的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间夹角为α,A、B两点之间的高度差与水平距离均为H,则以下判断中正确的是( )
空间某区域存在着电场,电场线在竖直面上的分布如图所示,一个质量为m、电量为q的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间夹角为α,A、B两点之间的高度差与水平距离均为H,则以下判断中正确的是( )
 空间某区域存在着电场,电场线在竖直面上的分布如图所示,一个质量为m、电量为q的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间夹角为α,A、B两点之间的高度差与水平距离均为H,则以下判断中正确的是( )
空间某区域存在着电场,电场线在竖直面上的分布如图所示,一个质量为m、电量为q的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间夹角为α,A、B两点之间的高度差与水平距离均为H,则以下判断中正确的是( )| A. | 小球由A点运动至B点,电场力做的功W=$\frac{1}{2}mv_2^2-\frac{1}{2}$mv12-mgH | |
| B. | A、B两点间的电势差U=$\frac{m}{2q}({v_2^2-v_1^2})$ | |
| C. | 带电小球由A运动到B的过程中,电场力对小球一定做正功 | |
| D. | 小球运动到B点时所受重力的瞬时功率为p=mgv2sinα |
15.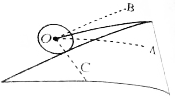 如图所示,要让光滑的球静止在光滑的斜面上,细绳的拉力和球的重力的合力方向一定是( )
如图所示,要让光滑的球静止在光滑的斜面上,细绳的拉力和球的重力的合力方向一定是( )
 如图所示,要让光滑的球静止在光滑的斜面上,细绳的拉力和球的重力的合力方向一定是( )
如图所示,要让光滑的球静止在光滑的斜面上,细绳的拉力和球的重力的合力方向一定是( )| A. | 沿OA方向 | B. | 沿OA到OB之间的某个方向 | ||
| C. | 沿OC方向 | D. | 沿OA到OC之间的某个方向 |
3.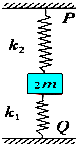 如图两个弹簧的质量不计,劲度系数分别为k1、k2,它们一端固定在质量为m的物体上,另一端分别固定在Q、P上,当物体平衡时上面的弹簧处于原长,若把固定的物体换为质量为2m的物体(弹簧的长度不变,且弹簧均在弹性限度内),当物体再次平衡时,物体比第一次平衡时的位置下降了x,则x为( )
如图两个弹簧的质量不计,劲度系数分别为k1、k2,它们一端固定在质量为m的物体上,另一端分别固定在Q、P上,当物体平衡时上面的弹簧处于原长,若把固定的物体换为质量为2m的物体(弹簧的长度不变,且弹簧均在弹性限度内),当物体再次平衡时,物体比第一次平衡时的位置下降了x,则x为( )
 如图两个弹簧的质量不计,劲度系数分别为k1、k2,它们一端固定在质量为m的物体上,另一端分别固定在Q、P上,当物体平衡时上面的弹簧处于原长,若把固定的物体换为质量为2m的物体(弹簧的长度不变,且弹簧均在弹性限度内),当物体再次平衡时,物体比第一次平衡时的位置下降了x,则x为( )
如图两个弹簧的质量不计,劲度系数分别为k1、k2,它们一端固定在质量为m的物体上,另一端分别固定在Q、P上,当物体平衡时上面的弹簧处于原长,若把固定的物体换为质量为2m的物体(弹簧的长度不变,且弹簧均在弹性限度内),当物体再次平衡时,物体比第一次平衡时的位置下降了x,则x为( )| A. | $\frac{mg}{{k}_{1}+{k}_{2}}$ | B. | $\frac{{k}_{1}{k}_{2}}{mg({k}_{1}+{k}_{2})}$ | ||
| C. | $\frac{2mg}{{k}_{1}+{k}_{2}}$ | D. | $\frac{{k}_{1}{k}_{2}}{2mg({k}_{1}+{k}_{2})}$ |
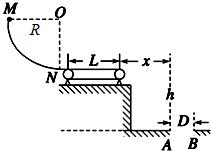 如图所示,半径R=0.2m的光滑四分之一圆轨道MN竖直固定放置,末端N与一长L=0.8m的水平传送带平滑相切,水平衔接部分无机械能损失,传动轮的轮半径很小,传送带以恒定的速度ν0作顺时针运动.传送带上表面离地面的高度h=1.25m,其右侧地面上有一直径D=0.5m的圆形洞,洞口最左端的A点离传送带右端的水平距离x=1m,B点在洞口的最右端.现使质量为m=0.5kg的小物块从M点由静止开始释放,经过传送带后做平抛运动,小物体视为质点,不计空气阻力,传送带与小物块之间的动摩擦因数μ=0.5.g取10m/s2.求:
如图所示,半径R=0.2m的光滑四分之一圆轨道MN竖直固定放置,末端N与一长L=0.8m的水平传送带平滑相切,水平衔接部分无机械能损失,传动轮的轮半径很小,传送带以恒定的速度ν0作顺时针运动.传送带上表面离地面的高度h=1.25m,其右侧地面上有一直径D=0.5m的圆形洞,洞口最左端的A点离传送带右端的水平距离x=1m,B点在洞口的最右端.现使质量为m=0.5kg的小物块从M点由静止开始释放,经过传送带后做平抛运动,小物体视为质点,不计空气阻力,传送带与小物块之间的动摩擦因数μ=0.5.g取10m/s2.求: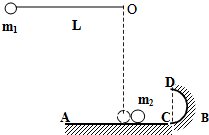 如图,一光滑水平桌面AB与一半径为R的光滑半圆形轨道相切于C点,且两者固定不动.一长L为0.8m的细绳,一端固定于O点,另一端系一个质量m1为0.2kg的球.当球在竖直方向静止时,球对水平桌面的作用力刚好为零.现将球提起使细绳处于水平位置时无初速释放.当球m1摆至最低点时,恰与放在桌面上的质量m2为0.8kg的小铁球正碰,碰后m1小球以2m/s的速度弹回,m2将沿半圆形轨道运动,恰好能通过最高点D.g=10m/s2,求
如图,一光滑水平桌面AB与一半径为R的光滑半圆形轨道相切于C点,且两者固定不动.一长L为0.8m的细绳,一端固定于O点,另一端系一个质量m1为0.2kg的球.当球在竖直方向静止时,球对水平桌面的作用力刚好为零.现将球提起使细绳处于水平位置时无初速释放.当球m1摆至最低点时,恰与放在桌面上的质量m2为0.8kg的小铁球正碰,碰后m1小球以2m/s的速度弹回,m2将沿半圆形轨道运动,恰好能通过最高点D.g=10m/s2,求