题目内容
如图所示，一个滑雪运动员，滑板和人总质量为m＝75kg，以初速度v0＝8m/s沿倾角为θ＝37°的斜坡向上自由滑行，已知滑板与斜坡间动摩擦因数μ＝0.25，假设斜坡足够长，不计空气阻力。试求：
（1）运动员沿斜坡上滑的最大距离；
（2）若运动员滑至最高点后掉转方向向下自由滑行，求他滑到起点时的速度大小。
（1）运动员沿斜坡上滑的最大距离；
（2）若运动员滑至最高点后掉转方向向下自由滑行，求他滑到起点时的速度大小。
解：（1）上滑过程中，对人进行受力分析，滑雪者受重力mg、弹力FN、摩擦力f，并设滑雪者加速度为
a1
a1
mgsinθ＋f＝ma1，a1方向沿斜面向下①
由平衡关系有：FN＝mgcosθ②
根据动摩擦定律有：f＝μFN③
由上列各式解得：a1＝g（sinθ＋μcosθ）＝8m/s2④
滑雪者沿斜面向上做匀减速直线运动，减速到为零时的位移x＝
＝4m⑤
即滑雪者上滑的最大距离为4m
（2）滑雪者沿斜面下滑时，滑雪者受到斜面的摩擦力沿斜面向上，设加速度大小为a2
由平衡关系有：FN＝mgcosθ②
根据动摩擦定律有：f＝μFN③
由上列各式解得：a1＝g（sinθ＋μcosθ）＝8m/s2④
滑雪者沿斜面向上做匀减速直线运动，减速到为零时的位移x＝
＝4m⑤ 即滑雪者上滑的最大距离为4m
（2）滑雪者沿斜面下滑时，滑雪者受到斜面的摩擦力沿斜面向上，设加速度大小为a2
根据牛顿第二定律有：mgsinθ－f＝ma2，a2方向沿斜面向下⑥
由平衡关系有：FN＝mgcosθ⑦
根据动摩擦定律有：f＝μFN⑧
由上列各式解得：a2＝g（sinθ－μcosθ）＝4m/s2⑨
滑雪者沿斜面向下做初速度为零的匀加速直线运动，滑到出发点的位移大小为x＝4m
则滑雪者再次滑到出发点时速度大小：v＝
＝4
m/s＝5.7m/s⑩
由平衡关系有：FN＝mgcosθ⑦
根据动摩擦定律有：f＝μFN⑧
由上列各式解得：a2＝g（sinθ－μcosθ）＝4m/s2⑨
滑雪者沿斜面向下做初速度为零的匀加速直线运动，滑到出发点的位移大小为x＝4m
则滑雪者再次滑到出发点时速度大小：v＝
＝4m/s＝5.7m/s⑩ 
练习册系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
如图所示，一个滑雪运动员保持图中姿势沿滑道下滑，滑行速度越来越小．不计空气阻力．下列说法正确的是（ ）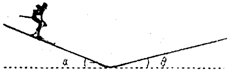
如图所示，一个滑雪运动员从左侧斜坡距离底8m处由静止滑下．以坡底为零势能参考面，当下滑到距离坡底s1处时，运动员的动能和势能恰好相等；到坡底后运动员又靠惯性冲上右侧斜坡．若不计经过坡底时的机械能损失，当上滑到距离坡底s2处时，运动员的动能和势能再次相等，上滑的最大距离为4m，在此全过程中，下列说法正确的是（ ）
（2007?南通模拟）如图所示，一个滑雪运动员从左侧斜坡距离坡底8m处自由滑下，当下滑到距离坡底s1处时，动能和势能相等（以坡底为参考平面）；到坡底后运动员又靠惯性冲上斜坡（不计经过坡底时的机械能损失），当上滑到距离坡底s2处时，运动员的动能和势能又相等，上滑的最大距离为4m．关于这个过程，下列说法中正确的是（ ）
如图所示，一个滑雪运动员保持图中姿势沿滑道下滑，滑行速度越来越小，不计空气阻力．下列说法中正确的是（ ）