题目内容
1.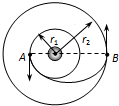 要发射一颗人造地球卫星,先将它发射到半径为r1、周期为T1的近地暂行轨道上绕地球做匀速圆周运动,在A点变轨到一个椭圆的转移轨道上,在远地点B时,再次变轨,使它进入半径为r2的预定轨道运行.则下列判断正确的是( )
要发射一颗人造地球卫星,先将它发射到半径为r1、周期为T1的近地暂行轨道上绕地球做匀速圆周运动,在A点变轨到一个椭圆的转移轨道上,在远地点B时,再次变轨,使它进入半径为r2的预定轨道运行.则下列判断正确的是( )| A. | 在近地暂行轨道上经过A点时需要加速才能进入椭圆轨道 | |
| B. | 在椭圆轨道上经过B点时需要减速才能进入预定圆轨道 | |
| C. | 在这三个轨道中,沿椭圆轨道运行时卫星的机械能最大 | |
| D. | 根据题中所给条件,即可求出卫星沿椭圆轨道运行一周的时间 |
分析 根据万有引力与向心力的关系确定如何变轨,根据功能关系确定哪个轨道机械能最大.根据开普勒第三定律求出卫星沿椭圆轨道运行的周期.
解答 解:A、在近地暂行轨道上经过A点时需要加速,使得万有引力小于向心力,做离心运动,进入椭圆轨道,故A正确.
B、椭圆轨道B点,由于万有引力大于向心力,将做近心运动,可在该点加速,使得万有引力等于向心力,进入圆轨道,故B错误.
C、由半径为r1的轨道进入椭圆轨道,需在A点加速,机械能增加,在椭圆轨道进入半径为r2的预定轨道也需要加速,机械能增加,在两个圆轨道和椭圆轨道上,机械能守恒,可知三个轨道中,半径为r2的预定轨道上机械能最大,故C错误.
D、根据开普勒第三定律,$\frac{{{r}_{1}}^{3}}{{{T}_{1}}^{2}}=\frac{(\frac{{r}_{1}+{r}_{2}}{2})^{3}}{{T}^{2}}$,可知能求出在椭圆轨道上的周期T.故D正确.
故选:AD.
点评 解决本题的关键知道变轨的原理,抓住万有引力和向心力的关系分析判断,以及会用开普勒第三定律解题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
11.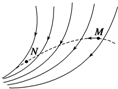 (多选)如图所示,实线表示电场线,虚线表示只受电场力作用的带正电粒子的运动轨迹,粒子先经过M点,再经过N点,可以判定( )
(多选)如图所示,实线表示电场线,虚线表示只受电场力作用的带正电粒子的运动轨迹,粒子先经过M点,再经过N点,可以判定( )
 (多选)如图所示,实线表示电场线,虚线表示只受电场力作用的带正电粒子的运动轨迹,粒子先经过M点,再经过N点,可以判定( )
(多选)如图所示,实线表示电场线,虚线表示只受电场力作用的带正电粒子的运动轨迹,粒子先经过M点,再经过N点,可以判定( )| A. | 粒子带负电 | |
| B. | 粒子的电势能不断减少 | |
| C. | 粒子的动能不断减少 | |
| D. | 粒子在M点的加速度小于在N点的加速度 |
9. 如图所示,物体质量为m,在沿斜面向上的拉力F作用下沿斜面匀速下滑,此过程中斜面仍静止,斜面质量为M,则水平面对斜面( )
如图所示,物体质量为m,在沿斜面向上的拉力F作用下沿斜面匀速下滑,此过程中斜面仍静止,斜面质量为M,则水平面对斜面( )
 如图所示,物体质量为m,在沿斜面向上的拉力F作用下沿斜面匀速下滑,此过程中斜面仍静止,斜面质量为M,则水平面对斜面( )
如图所示,物体质量为m,在沿斜面向上的拉力F作用下沿斜面匀速下滑,此过程中斜面仍静止,斜面质量为M,则水平面对斜面( )| A. | 无摩擦力 | B. | 有水平向左的摩擦力 | ||
| C. | 支持力为(M+m)g | D. | 支持力大于(M+m)g |
16.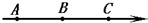 如图所示为电场中的某一条电场线,A、B、C是其上的三点.现用EA、EB、EC表示这三点的电场强度,ΦA、ΦB、ΦC表示这三点的电势,EPA、EPB、EPC表示某一点电荷-q在这三点具有的电势能,则必有( )
如图所示为电场中的某一条电场线,A、B、C是其上的三点.现用EA、EB、EC表示这三点的电场强度,ΦA、ΦB、ΦC表示这三点的电势,EPA、EPB、EPC表示某一点电荷-q在这三点具有的电势能,则必有( )
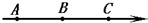 如图所示为电场中的某一条电场线,A、B、C是其上的三点.现用EA、EB、EC表示这三点的电场强度,ΦA、ΦB、ΦC表示这三点的电势,EPA、EPB、EPC表示某一点电荷-q在这三点具有的电势能,则必有( )
如图所示为电场中的某一条电场线,A、B、C是其上的三点.现用EA、EB、EC表示这三点的电场强度,ΦA、ΦB、ΦC表示这三点的电势,EPA、EPB、EPC表示某一点电荷-q在这三点具有的电势能,则必有( )| A. | EA>EB>EC | B. | ΦA>ΦB>ΦC | C. | EPA>EPB>EPC | D. | EPC=EPB=EPA |
6. 如图所示为粮袋的传送带装置,已知AB间的长度为L,传送带与水平方向的夹角为θ,工作时运行速度为v,粮袋与传送带间的动摩擦因数为μ,在传送带正常工作时,工人将粮袋轻轻放在A点,粮袋从A到B的运动过程中,以下说法正确的是 (设最大静摩擦力等于滑动摩擦力)( )
如图所示为粮袋的传送带装置,已知AB间的长度为L,传送带与水平方向的夹角为θ,工作时运行速度为v,粮袋与传送带间的动摩擦因数为μ,在传送带正常工作时,工人将粮袋轻轻放在A点,粮袋从A到B的运动过程中,以下说法正确的是 (设最大静摩擦力等于滑动摩擦力)( )
 如图所示为粮袋的传送带装置,已知AB间的长度为L,传送带与水平方向的夹角为θ,工作时运行速度为v,粮袋与传送带间的动摩擦因数为μ,在传送带正常工作时,工人将粮袋轻轻放在A点,粮袋从A到B的运动过程中,以下说法正确的是 (设最大静摩擦力等于滑动摩擦力)( )
如图所示为粮袋的传送带装置,已知AB间的长度为L,传送带与水平方向的夹角为θ,工作时运行速度为v,粮袋与传送带间的动摩擦因数为μ,在传送带正常工作时,工人将粮袋轻轻放在A点,粮袋从A到B的运动过程中,以下说法正确的是 (设最大静摩擦力等于滑动摩擦力)( )| A. | 粮袋到达B点的速度可能大于、等于或小于v | |
| B. | 粮袋开始运动的加速度为g(sinθ-?cosθ) | |
| C. | 若μ<tanθ,则粮袋从A到B一定一直是做加速运动 | |
| D. | 不论μ大小如何,粮袋从A到B一直匀加速运动,且a>gsinθ |
13. 如图所示,固定在水平面上的竖直轻弹簧上端与质量为M的物块A相连,静止时物块A位于P处.另有一质量为m的物块B,从A的正上方Q处自由下落,与A发生碰撞立即具有相同的速度,然后A、B一起向下运动,将弹簧继续压缩后,物块A、B被反弹.下面是有关的几个结论正确的是( )
如图所示,固定在水平面上的竖直轻弹簧上端与质量为M的物块A相连,静止时物块A位于P处.另有一质量为m的物块B,从A的正上方Q处自由下落,与A发生碰撞立即具有相同的速度,然后A、B一起向下运动,将弹簧继续压缩后,物块A、B被反弹.下面是有关的几个结论正确的是( )
 如图所示,固定在水平面上的竖直轻弹簧上端与质量为M的物块A相连,静止时物块A位于P处.另有一质量为m的物块B,从A的正上方Q处自由下落,与A发生碰撞立即具有相同的速度,然后A、B一起向下运动,将弹簧继续压缩后,物块A、B被反弹.下面是有关的几个结论正确的是( )
如图所示,固定在水平面上的竖直轻弹簧上端与质量为M的物块A相连,静止时物块A位于P处.另有一质量为m的物块B,从A的正上方Q处自由下落,与A发生碰撞立即具有相同的速度,然后A、B一起向下运动,将弹簧继续压缩后,物块A、B被反弹.下面是有关的几个结论正确的是( )| A. | A、B反弹过程中,在P处物块B与A相分离 | |
| B. | A、B反弹过程中,在P处物块B与A仍未分离 | |
| C. | B可能回到Q处 | |
| D. | B不可能回到Q处 |
10.某汽车以速度10m/s匀速行驶,刹车后第1个2s内位移与最后一个2s内位移之比为3:2,设汽车做匀减速直线运动,则刹车后4s内汽车通过的距离是( )
| A. | 2.5 m | B. | 4 m | C. | 12 m | D. | 12.5 m |
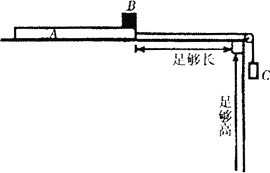 如图所示,在足够高的光滑水平台面上静置一质量为m的长木板A,A右端用轻绳绕过光滑的轻质定滑轮与质量也为m的物体C栓接.当C从静止开始下落距离h时,在木板A的最右端轻放一质量为4m的小铁块B(可视为质点),最终B恰好未从木板A上滑落.A、B间的动摩擦因数μ=0.25,且认为最大静摩擦力等于滑动摩擦力,重力加速度为g,求:
如图所示,在足够高的光滑水平台面上静置一质量为m的长木板A,A右端用轻绳绕过光滑的轻质定滑轮与质量也为m的物体C栓接.当C从静止开始下落距离h时,在木板A的最右端轻放一质量为4m的小铁块B(可视为质点),最终B恰好未从木板A上滑落.A、B间的动摩擦因数μ=0.25,且认为最大静摩擦力等于滑动摩擦力,重力加速度为g,求: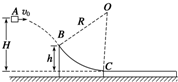 如图所示,从 A点以v0=4m/s的水平速度抛出一质量m=1kg的小物块(可视为质点),当小物块运动至B点时,恰好沿切线方向进入固定的光滑圆弧轨道BC,经圆弧轨道后滑上与C点等高、静止在光滑水平面的长木板上,圆弧轨道C端切线水平.已知长木板的质量M=4kg,A、B两点距C点的高度分别为H=0.6m、h=0.15m,R=0.75m,小物块与长木板之间的动摩擦因数μ1=0.5,g=10m/s2.求:
如图所示,从 A点以v0=4m/s的水平速度抛出一质量m=1kg的小物块(可视为质点),当小物块运动至B点时,恰好沿切线方向进入固定的光滑圆弧轨道BC,经圆弧轨道后滑上与C点等高、静止在光滑水平面的长木板上,圆弧轨道C端切线水平.已知长木板的质量M=4kg,A、B两点距C点的高度分别为H=0.6m、h=0.15m,R=0.75m,小物块与长木板之间的动摩擦因数μ1=0.5,g=10m/s2.求: