题目内容
如图所示，两根完全相同的弹簧下挂一质量为m的小球，小球与地面间有细线相连，处于静止状态，细线竖直向下的拉力大小为2mg．若剪断细线，则在剪断细线的瞬间，小球的加速度a为
- A.a=g 方向竖直向上
- B.a=g 方向竖直向下
- C.a=2g 方向竖直向上
- D.a=3g 方向竖直向上
C
分析：根据共点力平衡求出两根弹簧的合力，剪断细线的瞬间，弹簧弹力不变，根据牛顿第二定律求出小球的加速度大小和方向．
解答：开始小球处于平衡状态，两根弹簧弹力的合力等于重力和绳子的拉力之和，即两根弹簧弹力的合力F1=T+mg=3mg．
剪断细线的瞬间，弹簧弹力不变，根据牛顿第二定律得，a=
，方向竖直向上．故C正确，A、B、D错误．
故选C．
点评：本题考查了共点力平衡和牛顿第二定律的基本运用，知道剪断细线的瞬间，弹簧的弹力不变，结合牛顿第二定律求解瞬时加速度．
分析：根据共点力平衡求出两根弹簧的合力，剪断细线的瞬间，弹簧弹力不变，根据牛顿第二定律求出小球的加速度大小和方向．
解答：开始小球处于平衡状态，两根弹簧弹力的合力等于重力和绳子的拉力之和，即两根弹簧弹力的合力F1=T+mg=3mg．
剪断细线的瞬间，弹簧弹力不变，根据牛顿第二定律得，a=
，方向竖直向上．故C正确，A、B、D错误．故选C．
点评：本题考查了共点力平衡和牛顿第二定律的基本运用，知道剪断细线的瞬间，弹簧的弹力不变，结合牛顿第二定律求解瞬时加速度．
练习册系列答案
相关题目
我国发射的“神州六号”载人宇宙飞船绕地球运动的周期约为90min．如果把它绕地球的运动看作是匀速圆周运动，该飞船的运动和在轨道上运行的地球同步卫星的运动相比较，该飞船的轨道半径
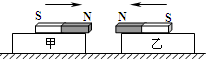
（2008?绵阳模拟）如图所示，在磁感应强度大小为B、方向竖直向上的匀强磁场中，有两根本身不相连接的光滑金属导轨处在竖直平面内，构成与水平面平行的上、下两层．在两水平导轨面上各放一根完全相同的质量为m的匀质金属杆1 和2，开始时两根金属杆都与轨道垂直，分别静止在a 处和c 处．两导轨面相距为h，导轨间宽为L，导轨足够长且电阻不计，每根金属杆电阻为r．现给金属杆1 一个水平向右的冲量使它具有初速度v0，金属杆1 离开右端b 时金属杆2 正好在b 的正下方d 处，金属杆1 落在下层导轨的e 处．d 与e 之间的距离为S．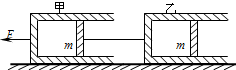
如图所示，光滑水平面上放置甲、乙两个内外壁都光滑的完全相同的气缸，气缸内各有一质量为m的活塞，密封完全相同的两部分气体（分子力可以忽略），甲、乙间用一根轻质水平细线相连接．现对甲气缸施一水平向左的恒定拉力F作用，甲气缸内气体的压强为p1，体积为V1；乙气缸内气体的压强为p2，体积为V2．设两部分气体始终和环境的温度相同，则（ ）
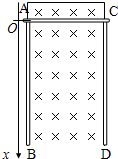如图所示，AB和CD是两根特制的、完全相同的电阻丝导轨，固定在绝缘的竖直墙壁上，上端用电阻不计的导线相连接，两电阻丝导轨相距为L，一根质量为m、电阻不计的金属棒跨接在AC间，并处于x轴原点，与电阻丝导轨接触良好，且无摩擦，空间有垂直墙面向里的匀强磁场，磁感应强度为B．放开金属棒，它将加速下滑．