��Ŀ����
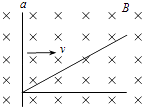
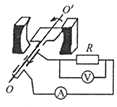
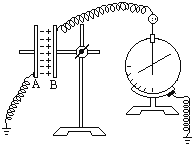
����Ŀ����ͼ��ʾ�����費�ƵĹ⻬��������ABC��DEFƽ�з��ã����ΪL��BC��EFˮƽ��AB��DE��ˮƽ��ɦȽǣ�PQ��P��Q����������Ϊm�������ΪR�Ľ����ˣ������뵼�촹ֱ��ƽ�а�������������壨���Ϊd��M��Nˮƽ���ã���ͨ�������뵼�����ӣ�FC��������������ڴŸ�Ӧǿ�ȴ�СΪB1��������ֱ���µ���ǿ�ų��У��������������Բ�������ڴ��ڴ�ֱ��ֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB2 �� Բ�δų�����뾶r1=0.5d������������弰����Ե�����У��ø�PQ��ˮƽ�����˶���ʹ��P��Q�侲ֹ����������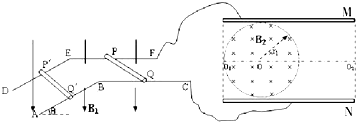
��1��PQ�˶��ٶȵĴ�С�ͷ���
��2����һ�����������Ĵ����������������������O1O2������Ե��O1�����ٶ�v0���룬ǡ��ֱ��ͨ��Բ�δų�������ʱ��t0�Ӽ����Ե�ɳ�����ȥ�ų����ø������Դ�O1������ͬ�ٶ����룬��t0/2ʱ������ϣ���v0�Ĵ�СΪ���٣�
��3���������岻���磬����Բ������ų����䣬���㣨2���ʱȺɵĸ���������������O1O2��O1�����룬��ʹ���Ӵ������ɳ�����������ٶȴ�СӦ���������[��֪tan2��= ![]() ]��
]��
���𰸡�
��1��
�⣺PQ�и�Ÿ��߲����ĸ�Ӧ�綯�ƣ�E=B1Lv��
��·������I= ![]() =
= ![]() ��
��
P��Q����ܵ��İ�������F=B1IL= ![]() ��
��
P��Q��˾�ֹ����ƽ��״̬����ƽ�������ã�mgtan��=F��
��ã�v= ![]() ��
��
�����ֶ��������ֶ����֪��PQӦ�����˶�
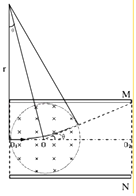
��2��
�⣺�輫�峤Ϊx����ȥ�ų�����������ƽ���˶���ˮƽ����λ�ƣ�x��2r1=x��d��
�дų�ʱ��x=v0t0���ų�ʱ��x��d= ![]() ��
��
��ã�x=2d��v0= ![]()
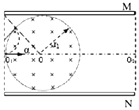
��3��
�⣺��ȥ�ų�ʱ��������ƽ���˶������ӵ�ƫ������0.5d= ![]()
![]()
![]() ��
��
�����ڴų���������ֱ���˶�����ƽ�������ã�qv0B2=q ![]() ��
��
��ã� ![]() =
= ![]() ��
��
�糡ʱ�����ڴų���������Բ���˶�������ǡ�ô��ϼ������Եʱ�Ĺ���뾶Ϊr��Բ�Ľ�Ϊ����
�ɼ���֪ʶ�ã�tan��= ![]() ����=45�㣬r+
����=45�㣬r+ ![]() r=0.5d��
r=0.5d��
���������ṩ����������ţ�ٵڶ����ɵã�qvB2=m ![]() ��
��
��ã�v= ![]() ��
��
����ǡ�ô��ϼ����ұ�Ե�ɳ�ʱ���ɼ���֪ʶ�ã�
tan2��= ![]() ��tan��=
��tan��= ![]() ����֪��tan2��=
����֪��tan2��= ![]() ��
��
��ã�v= ![]() ��
��
���ӵ��ٶ���Ҫ����������ǣ�0��v�� ![]() ��v��
��v�� ![]()
����������1��Ӧ��E=BLv�����Ӧ�綯�ƣ�Ӧ��ŷķ�������������Ӧ�ð�������ʽ������ܵ��İ�������Ȼ��Ӧ��ƽ����������˵��ٶȴ�С��Ӧ�����ֶ��������ֶ����жϸ˵��˶�����2����ȥ�ų�ʱ��������ƽ���˶����дų�ʱ����������ֱ���˶���Ӧ����ƽ���˶�������ƽ����������������ӵ��ٶȣ���3�������ڴų���������Բ���˶������������ṩ��������������ӵ��ٽ��ٶȣ�Ȼ��ȷ�����ٶȷ�Χ��
�����㾫�������ڱ��⿼���������������Ҫ�˽���������ʼ�մ�ֱ��v�ķ���������������һ�����������ܵó���ȷ�𰸣�