题目内容
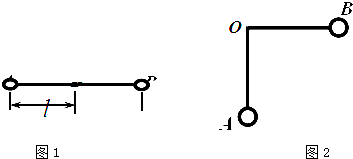
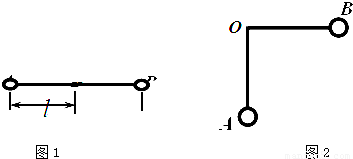
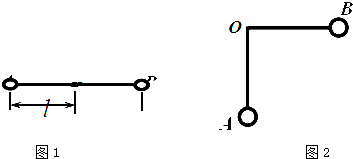
如图1所示,在竖直向下,场强为E的匀强电场中,长为2l的绝缘轻杆可绕固定轴O在竖直平面内无摩擦转动,两个小球A、B固定于杆的两端,A、B的质量分别为m1和m2,A带负电,电量为q1,B也带负电,电量为q2.求:
(1)杆从静止开始由水平位置顺时针转到竖直位置,在此过程中电场力所做的功为多少?
(2)杆从静止开始由水平位置顺时针转到竖直位置时,两球的总动能为多少?
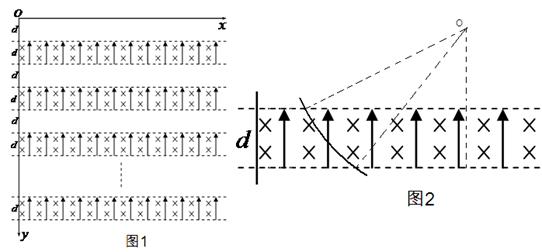
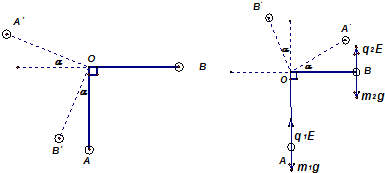
(3)若将轻杆弯折成如图2所示的“Γ”形,两边互相垂直、长度均为l,在竖直向下的匀强电场中(场强E的大小未知),可绕过O点的水平轴在竖直平面内无摩擦转动.现将“Γ”形杆从OB位于水平位置由静止释放,OB杆能转过的最大角度为127°,则该电场强度的大小为多少?
(1)杆从静止开始由水平位置顺时针转到竖直位置,在此过程中电场力所做的功为多少?
(2)杆从静止开始由水平位置顺时针转到竖直位置时,两球的总动能为多少?
(3)若将轻杆弯折成如图2所示的“Γ”形,两边互相垂直、长度均为l,在竖直向下的匀强电场中(场强E的大小未知),可绕过O点的水平轴在竖直平面内无摩擦转动.现将“Γ”形杆从OB位于水平位置由静止释放,OB杆能转过的最大角度为127°,则该电场强度的大小为多少?

(1)电场力做功大小W=Eq1l-Eq2l
(2)对系统研究,根据动能定理得:( q1-q2)El+(m2-m1)g l=Ek-0
解得:Ek=( q1-q2)El+(m2-m1)g l
(3)OB杆可能顺时针转动,也可能逆时针转动.当OB杆转过最大角度时,动能为零.
(ⅰ)设OB杆顺时针转动,根据动能定理,
(m2g-q2 E)l cosα-( q1E-m1g)l(1+sinα)=0
解得:E=
g<
讨论:由于使OB杆顺时针转动,
必须满足m2g>q2E,
所以:E=
g<
即:
-
<0
<0
当q2>2q1,
>
时,顺时针转动,当 q2<2q1,
<
时,顺时针转动.
(ⅱ)设OB杆逆时针转动,根据动能定理,
(q2E-m2 g)lcosα+(q1E-m1g)l(1+sinα)=0
解得:E=
g>
讨论:由于使OB杆逆时针转动,必须满足m2g<q2E,
所以:E=
g>
即:
-
g>0
>0
当 m1q2>m2q1时,即当
>
时杆逆时针转动.
答:(1)杆从静止开始由水平位置顺时针转到竖直位置,在此过程中电场力所做的功为Eq1l-Eq2l.
(2)两球的总动能为( q1-q2)El+(m2-m1)g l.
(3)当顺时针转动时,该电场强度的大小为
g,逆时针转动时,电场强度的大小为
g.
(2)对系统研究,根据动能定理得:( q1-q2)El+(m2-m1)g l=Ek-0
解得:Ek=( q1-q2)El+(m2-m1)g l
(3)OB杆可能顺时针转动,也可能逆时针转动.当OB杆转过最大角度时,动能为零.
(ⅰ)设OB杆顺时针转动,根据动能定理,
(m2g-q2 E)l cosα-( q1E-m1g)l(1+sinα)=0
解得:E=
| m2-2m1 |
| q2-2q1 |
| m2g |
| q2 |
讨论:由于使OB杆顺时针转动,
必须满足m2g>q2E,

所以:E=
| m2-2m1 |
| q2-2q1 |
| m2g |
| q2 |
即:
| m2-2m1 |
| q2-2q1 |
| m2 |
| q2 |
| 2(m2q1-m1q2) |
| q2(q2-2q1) |
当q2>2q1,
| m1 |
| m2 |
| q1 |
| q2 |
| m1 |
| m2 |
| q1 |
| q2 |
(ⅱ)设OB杆逆时针转动,根据动能定理,
(q2E-m2 g)lcosα+(q1E-m1g)l(1+sinα)=0
解得:E=
| m2+2m1 |
| q2+2q1 |
| m2g |
| q2 |
讨论:由于使OB杆逆时针转动,必须满足m2g<q2E,
所以:E=
| m2+2m1 |
| q2+2q1 |
| m2g |
| q2 |
即:
| m2+2m1 |
| q2+2q1 |
| m2 |
| q2 |
| 2(m1q2-m2q1)g |
| q2(q2+2q1) |
当 m1q2>m2q1时,即当
| m1 |
| m2 |
| q1 |
| q2 |
答:(1)杆从静止开始由水平位置顺时针转到竖直位置,在此过程中电场力所做的功为Eq1l-Eq2l.
(2)两球的总动能为( q1-q2)El+(m2-m1)g l.
(3)当顺时针转动时,该电场强度的大小为
| m2-2m1 |
| q2-2q1 |
| m2+2m1 |
| q2+2q1 |

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目