题目内容
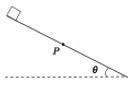
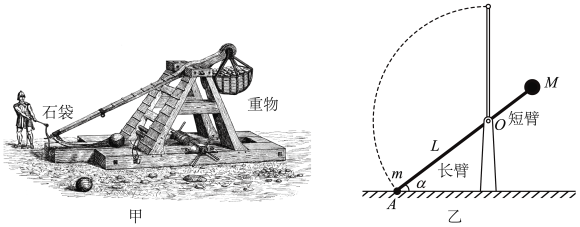
【题目】如图甲所示为历史上著名的襄阳炮,因在公元1267-1273年的宋元襄阳之战中使用而得名,其实质就是一种大型抛石机。它采用杠杆式原理,由一根横杆和支架构成,横杆的一端固定重物,另一端放置石袋,发射时用绞车将放置石袋的一端用力往下拽,而后突然松开,因为重物的牵缀,长臂会猛然翘起,石袋里的巨石就被抛出。将其工作原理简化为图乙所示,横杆的质量不计,将一质量m=10kg,可视为质点的石块,装在横杆长臂与转轴O点相距L=5m的末端口袋中,在转轴短臂右端固定一重物M,发射之前先利用外力使石块静止在地面上的A点,静止时长臂与水平面的夹角α=37°,解除外力后石块被发射,当长臂转到竖直位置时立即停止运动,石块被水平抛出,落在水平地面上,石块落地位置与O点的水平距离s=20m,空气阻力不计,g取10m/s2。则( )
A.石块水平抛出时的初速度为l0![]() m/s
m/s
B.石块水平抛出时的初速度为20m/s
C.从A点到最高点的过程中,长臂对石块做的功为2050J
D.从A点到最高点的过程中,长臂对石块做的功为2500J
【答案】C
【解析】
AB.石块被抛出后做平抛运动,竖直高度为
![]()
可得

水平方向匀速直线运动
![]()
可得平抛的初速度为
![]()
故AB错误;
C D.石块从A点到最高点的过程,由动能定理
![]()
解得长臂对石块做的功为
![]()
故C正确,D错误。
故选C。

练习册系列答案
相关题目