题目内容
 如图所示,两块平行金属板,相距为d.加上如图所示的电压,电压的最大值为U,周期为T.现有一束离子束,其中每个粒子的电量为q、质量为m,从与两板等距处沿两板平行的方向连续射入,设粒子通过平行板间区域所用的时间为T(与电压的变化周期相同),且所有的粒子都可以通过两板间的空间而打到右端的靶上.
如图所示,两块平行金属板,相距为d.加上如图所示的电压,电压的最大值为U,周期为T.现有一束离子束,其中每个粒子的电量为q、质量为m,从与两板等距处沿两板平行的方向连续射入,设粒子通过平行板间区域所用的时间为T(与电压的变化周期相同),且所有的粒子都可以通过两板间的空间而打到右端的靶上.
(1)粒子打到靶上的位置与靶的中心点O间的距离s与粒子入射时刻t有关,写出s与t[t![]() ]的函数关系式.
]的函数关系式.
(2)求所有粒子打到靶上的位置的范围(即求出它们与靶的中心点O的最大距离与最小距离).
(1)s(t)=![]() [t
[t![]() ].
].
(2)当t=0时,得最大值smax=![]() ,当t=T/2时,得最小值smin=
,当t=T/2时,得最小值smin=![]()
解析:
带电粒子射入两板间,若无电场,将沿水平直线做匀速运动,若有电场,在水平方向仍做匀速直线运动,而在竖直方向,将做匀加速运动,加速度大小为a=Uq/dm,方向向下.已知所有粒子通过此区域所用时间都是T,说明粒子的初速度大小都相等.但在这1个周期时间内,总有半个周期有电场,另半个周期没有电场.粒子射入的时刻不同,运动情况也有不同,我们作出t=0时刻(甲)及任意时刻t射入的粒子(乙)的竖直方向分速度v1随时间t变化的图像,如图所示.比较甲、乙二粒子的图像,可以看出,甲前半个周期做匀加速运动,速度v1增至最大,后半个周期则以速度v1做匀速运动;乙的匀加速运动分为两段,中间的半个周期做匀速运动,我们把乙的加速运动两段合并起来,与甲的相同,二者不同之处就于做匀速运动半个周期的速度大小不同.
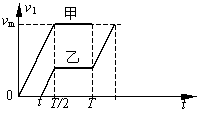
甲粒子在竖直方向总位移sm=![]() .
.
乙粒子在竖直方向总位移s(t)=![]() .
.
(1)粒子打到靶上的位置与靶的中心点O间的距离s与粒子入射时刻t有关,写出s与t[t![]() ]的函数关系式为
]的函数关系式为
s(t)=![]() [t
[t![]() ].
].
(2)当t=0时,得最大值smax=![]() ,当t=T/2时,得最小值smin=
,当t=T/2时,得最小值smin=![]()

 科学实验活动册系列答案
科学实验活动册系列答案
 如图甲所示,A,B为两块平行金属板,板中央均有小孔,M、N是两块与B板垂直的平行金 属板,与M和N板等距离的中间轴线(图中虚线)通过0孔.M、N板长L=2X 1O -2m,板间距离d=4x10-3m,两板间所加电压U0=20V,在两板间形成匀强电场.一束电子 以初动能E0=120eV,从A板上的小孔0不断垂直于板射入A、B之间,现在A、B两板间 加一个如图乙所示的作周期性变化的电压U,在t=0到t=2s时间内A板电势高于B板 电势,则从t=0到t=4s的时间内.
如图甲所示,A,B为两块平行金属板,板中央均有小孔,M、N是两块与B板垂直的平行金 属板,与M和N板等距离的中间轴线(图中虚线)通过0孔.M、N板长L=2X 1O -2m,板间距离d=4x10-3m,两板间所加电压U0=20V,在两板间形成匀强电场.一束电子 以初动能E0=120eV,从A板上的小孔0不断垂直于板射入A、B之间,现在A、B两板间 加一个如图乙所示的作周期性变化的电压U,在t=0到t=2s时间内A板电势高于B板 电势,则从t=0到t=4s的时间内.
 )如图13所示,两块平行金属板A、B水平放置,板间距离为d,两金属板分别与电源的正、负极相连接。在距离B板d/2处的O点有一个质量为m的带电液滴恰好保持静止状态,液滴所带电荷为q。
)如图13所示,两块平行金属板A、B水平放置,板间距离为d,两金属板分别与电源的正、负极相连接。在距离B板d/2处的O点有一个质量为m的带电液滴恰好保持静止状态,液滴所带电荷为q。