题目内容
12. 如图,一轻质弹簧一端固定、另一端与质量为M的小滑块连接,开始时滑块静止在水平导轨的O点,弹簧处于原长状态.导轨的OA段是粗糙的,其余部分都是光滑的.有一质量为m的子弹以大小为v的速度水平向右射入滑块,并很快停留在滑块中.之后,滑块先向右滑行并越过A点,然后再向左滑行,最后恰好停在出发点O处.
如图,一轻质弹簧一端固定、另一端与质量为M的小滑块连接,开始时滑块静止在水平导轨的O点,弹簧处于原长状态.导轨的OA段是粗糙的,其余部分都是光滑的.有一质量为m的子弹以大小为v的速度水平向右射入滑块,并很快停留在滑块中.之后,滑块先向右滑行并越过A点,然后再向左滑行,最后恰好停在出发点O处.(1)求滑块滑行过程中弹簧弹性势能的最大值.
(2)滑块停在O点后,另一质量也为m的子弹以另一速度水平向右射入滑块并很快停留在滑块中,此后滑块滑行过程先后有两次经过O点.求第二颗子弹入射前的速度u的大小在什么范围内?
分析 (1)一颗子弹射入滑块后,根据动量守恒定律求出速度.滑块向右滑行至最右端时,弹簧弹性势能达到最大,由能量守恒定律列出方程.滑块由最右端向左滑行至O点,再由功能关系得到弹簧的弹性势能与OA段的长度的关系式,联立求出弹簧弹性势能的最大值.
(2)由动量守恒定律求出第二颗子弹射入滑块后滑块的速度,若滑块第一次返回O点时就停下,根据能量守恒定律求出速度u;若滑块第一次返回O点后继续向左滑行,再向右滑行,且重复第一次滑行过程,最后停在O点,由能量守恒定律求出速度u,联立即可得到速度u的范围.
解答 解:(1)设OA段的长度为l,与滑块间的动摩擦因数为μ,设第一颗子弹射入滑块后滑块的速度为v1,
由动量守恒定律得 mv=(M+m)v1 ①
滑块向右滑行至最右端时,弹簧弹性势能达到最大,设为EP,由功能关系得
$\frac{1}{2}$(M+m)v12=μ(M+m)?gl+EP ②
滑块由最右端向左滑行至O点,由功能关系得
EP=μ(M+m)gl ③
解得:${E_P}=\frac{{{m^2}{v^2}}}{4(M+m)}$④
(2)设第二颗子弹射入滑块后滑块的速度为v2,
由动量守恒定律得 mu=(M+2m)v2 ⑤
若滑块第一次返回O点时就停下,则滑块的运动情况与前面的情况相同
$\frac{1}{2}$(M+2m)v22=μ(M+2m)g?2l ⑥
解得$u=\frac{M+2m}{M+m}v$⑦
若滑块第一次返回O点后继续向左滑行,再向右滑行,且重复第一次滑行过程,最后停在O点,则$\frac{1}{2}$(M+2m)v22=μ(M+2m)g?4l ⑧
解得$u=\frac{M+2m}{M+m}\sqrt{2}v$⑨
第二颗子弹入射前的速度u 的大小在以下范围内$\frac{M+2m}{M+m}v<u<\frac{M+2m}{M+m}\sqrt{2}v$
答:(1)滑块滑行过程中弹簧弹性势能的最大值为$\frac{{m}^{2}{v}^{2}}{4(M+m)}$.
(2)第二颗子弹入射前的速度u的大小范围为$\frac{M+2m}{M+m}v<u<\frac{M+2m}{M+m}\sqrt{2}v$.
点评 本题考查了动量守恒定律和能量守恒关系在子弹打木块模型中的应用,注意研究对象的选取和能量守恒关系的应用,要挖掘隐含的临界条件,确定速度u的速度范围.

 学业测评一课一测系列答案
学业测评一课一测系列答案| A. | 乙比甲先落地 | B. | 甲、乙一定同时落地 | ||
| C. | 乙的加速度比甲的大 | D. | 甲球落地时的速度比乙的大 |
| A. | 物体的速度越大,其加速度也越大 | |
| B. | 物体的加速度大,其速度一定大 | |
| C. | 物体的速度变化量越大,其加速度就越大 | |
| D. | 物体的速度变化越快,其加速度就越大 |
| A. | 物体的两个分运动是直线运动,则它们的合运动一定是直线运动 | |
| B. | 若两个分运动分别是匀速直线运动和匀加速直线运动,则合运动可能是曲线运动 | |
| C. | 两个分运动的时间之和与它们合运动的时间相等 | |
| D. | 速度、加速度和位移的合成都遵循平行四边形定则 |
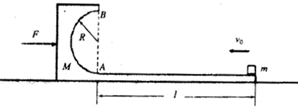 光滑水平面上,一个水平长木板与半径R未知的半圆组成如图所示的装置,装置质量M=5kg.在装置的右端放一质量为m=1kg的小滑块(可视为质点),小滑块与长木板间的动摩擦因数μ=0.5,装置与小滑块一起以v0=10m/s的速度向左运动.现给装置加一个F=55N向右的水平推力,小滑块与木板发生相对滑动,当小滑块滑至长木板左端A时,装置速度恰好减速为0,此时撤去外力F并将装置锁定不动.小滑块继续沿半圆形轨道运动,且恰好能通过轨道最高点B.滑块脱离半圆形轨道后又落回长木板.已知小滑块在通过半圆形轨道时克服摩擦力做功Wf=2.5J.g取10m/s2.求:
光滑水平面上,一个水平长木板与半径R未知的半圆组成如图所示的装置,装置质量M=5kg.在装置的右端放一质量为m=1kg的小滑块(可视为质点),小滑块与长木板间的动摩擦因数μ=0.5,装置与小滑块一起以v0=10m/s的速度向左运动.现给装置加一个F=55N向右的水平推力,小滑块与木板发生相对滑动,当小滑块滑至长木板左端A时,装置速度恰好减速为0,此时撤去外力F并将装置锁定不动.小滑块继续沿半圆形轨道运动,且恰好能通过轨道最高点B.滑块脱离半圆形轨道后又落回长木板.已知小滑块在通过半圆形轨道时克服摩擦力做功Wf=2.5J.g取10m/s2.求: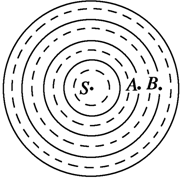 如图所示为由波源S发出的波某一时刻在介质平面中的情形,实线为波峰,虚线为波谷,设波源频率为20Hz,且不运动,而观察者在1s内由A运动到B,观察者接收到19个完全波.
如图所示为由波源S发出的波某一时刻在介质平面中的情形,实线为波峰,虚线为波谷,设波源频率为20Hz,且不运动,而观察者在1s内由A运动到B,观察者接收到19个完全波.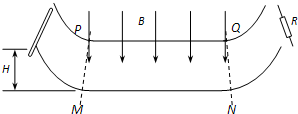
 在测定电流表内阻的实验中,备用的器材有:
在测定电流表内阻的实验中,备用的器材有: 如图所示,水平桌面的右端固定一定滑轮,轻质小盘通过一根绕过定滑轮的轻质细绳与桌面上的木块相连.当小盘内放有重为0.5N的砝码时,木块未被拉动,这时木块受到的摩擦力大小为0.5N;当小盘内放有重为0.6N的砝码时,木块正好作匀速运动,当小盘内放上重为0.7N的砝码时,小盘拖动木块运动,当小盘落在地面上后,木块继续运动,此时木块所受到的摩擦力大小为0.6N.
如图所示,水平桌面的右端固定一定滑轮,轻质小盘通过一根绕过定滑轮的轻质细绳与桌面上的木块相连.当小盘内放有重为0.5N的砝码时,木块未被拉动,这时木块受到的摩擦力大小为0.5N;当小盘内放有重为0.6N的砝码时,木块正好作匀速运动,当小盘内放上重为0.7N的砝码时,小盘拖动木块运动,当小盘落在地面上后,木块继续运动,此时木块所受到的摩擦力大小为0.6N.